Биссектриса угла bad параллелограмма abcd пересекает сторону bc в точке n, а биссектрису dm (точка м лежит на стороне bc) угла adc в точке о, причём точка о лежит внутри параллелограмма abcd. периметр параллелограмма abcd равен 64 и dn: nc=7: 2. найдите длину отрезка mn

Показать ответ

Ответ:

Aleksandr31821

16.06.2020 12:28

Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: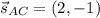 $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: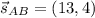 $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$

Даны уравнения прямых, содержащих высоты треугольника, и координаты одной из вершин треугольника. вы

0,0(0 оценок)

Ответ:

marinamih

16.06.2020 12:28

Площадь параллелограмма равна произведению смежных сторон на синус угла между ними:
S = ab·sinA
По теореме косинусов квадрат диагонали равен:
d² = a² + b² - 2ab·cosA
cosA = √1 - sin²A = √1 - 9/25 = 4/5
18 = a² + b² - 8/5ab (1)

3 = 3/5ab
ab = 5
Подставляем ab = 5 в (1) равенство
18 = a² + b² - 8/5·5
a² + b² - 8 = 18
a² + b² = 26
Выделим полный квадрат:
a² + 2ab + b² - 2ab = 26
(a + b)² - 2·5 = 26
(a + b)² = 36

a + b = 6
a·b = 5

По обратной теореме Виета:
a = 5, b = 1 или a = 1, b = 5

P = 2(a + b) = 2(5 + 1) = 12
ответ: 12.

0,0(0 оценок)

Популярные вопросы: Геометрия