1 у них один угол напротив лежащий и две стороны одинаковые , всё они подобны по одному углу и двум сторонам
3 там не всё видно но я предпологаю что там ещё одни углы равны поэтому треугольники равны по стороне и двум углам т к снизу два угла равны одни из сторон равны и тот угл
4 одни из сторон равны и равны одни углы и т к это параллелограмм то у них противоположные углы равны поэтому эти треугольники равны по одной стороне и двум углам
11 там вообще легко даётся что две стороны равны осталось найти угл между ними и их можно найти 180градусов - те углы которые на плоскости и всё и треугольники равны по двум сторонам и углу между ними
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 * *h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
1 у них один угол напротив лежащий и две стороны одинаковые , всё они подобны по одному углу и двум сторонам
3 там не всё видно но я предпологаю что там ещё одни углы равны поэтому треугольники равны по стороне и двум углам т к снизу два угла равны одни из сторон равны и тот угл
4 одни из сторон равны и равны одни углы и т к это параллелограмм то у них противоположные углы равны поэтому эти треугольники равны по одной стороне и двум углам
11 там вообще легко даётся что две стороны равны осталось найти угл между ними и их можно найти 180градусов - те углы которые на плоскости и всё и треугольники равны по двум сторонам и углу между ними
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 *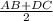
*h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
равновеликих треугольника) = 1/2*S(СDFE)=1/2*10=5 (см²).
S(DAEF)=S(DAE)-S(DFE)=19-5=14 (см²) .