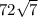Правильная четырехугольная пирамида - когда в ее основании лежит квадрат, а грани - четыре равных равнобоких треугольника. Высота пирамиды, ее боковое ребро и половина диагонали основания(квадрата) образуют прямоугольный тр-к, в котором против угла 30 лежит катет (половина диагонали основания(квадрата)) , равный половине гипотенузы (ребра).
В нашем случае половина диагонали квадрата по Пифагору равна √72, значит ребро равно 2√72. Тогда высота грани по Пифагору равна √288-36 = √252= 6√7. Площадь грани равна 1\2*12*6√7 = 36√7. Таких граней 4, площадь боковой поверхности пирамиды = 144√7 = 381.
Правильная четырехугольная пирамида - когда в ее основании лежит квадрат, а грани - четыре равных равнобоких треугольника. Высота пирамиды, ее боковое ребро и половина диагонали основания(квадрата) образуют прямоугольный тр-к, в котором против угла 30 лежит катет (половина диагонали основания(квадрата)) , равный половине гипотенузы (ребра).
В нашем случае половина диагонали квадрата по Пифагору равна √72, значит ребро равно 2√72. Тогда высота грани по Пифагору равна √288-36 = √252= 6√7. Площадь грани равна 1\2*12*6√7 = 36√7. Таких граней 4, площадь боковой поверхности пирамиды = 144√7 = 381.
(если не ошибся в арифметике)
Найдём диагональ основания и высоту пирамиды:
d - диагональ
h - высота
d=2*cos(60)*12=12
a - сторона основания
a=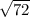
h = sin(60)*12=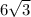
b - высота боковой грани
S = 4*0.5*b *a =2*b*a=