Боковое ребро правильной шестиугольной пирамиды равно 12 и наклонено к плоскости основания под углом 60°. найдите сторону основания пирамиды. найдите площадь полной поверхности пирамиды​

АВСД трапеция. ВС- меньшее основание. АВ = ВС = СД поскольку трапеция равнобокая и ее меньшее основание равно боковой стороне. АС - диагональ. Угол САД = 30 градусов. Это все по условию задачи.
Решение.
Треуг. АВС равнобедреннй, поскольку АВ = ВС, значит Угол ВАС = ВСА.
Угол САД = ВСА как накрест лежащие при параллельных прямых ВС и АД и секущей АС. Значит ВАС = 30 градусов, т.е АС является биссектрисой угла ВАД. Тогда угол ВАД = 30 + 30 =60 градусов.
Углы ВАД и АВС являются внутренними односторонними при параллельных прямых ВС и АД и секущей АВ. А сумма внутренних односторонних углов при двух параллельных прямых и секущей равна 180 градусов.
Угол АВС = 180 - 60 = 120 градусов.
Поскольку трапеция равнобокая, то
угол ВАД = СДА = 60 градусов
угол АВС = ВСД = 120 градусов.

S бічної поверхні = сантиметрів квадратних

Объяснение:

Дано:  Правильна шестикутна піраміда, R = 5 см, α = 30°(α - бічні грані правильної шестикутної піраміди нахилені до основи під кутом α)

Знайти:

S - ?(площу бічної поверхні)

Розв'язання: Розглянемо правильний шестикутник ABCDEF. Проведемо відрізки OD і OE і розглянемо трикутник Δ DOE, який буде рівнобедренним тому, що OD = OE (OD = OE = 5см за умовою), як радіуси описаного кола.Позначимо середину відрізка DE у точці M і з вершини O проведемо відрізок OM - який буде медіаною. За умовою ∠HMO = α.За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, а так як OM⊥DE, то OM є радіусом вписаного кола.У правильного шестикутника 6 сторін, а отже шість центральних кутів, нехай центральний кут β, тоді ∠DOE = β, усі 6 центральних кутів утворють повне коло отже ∠DOE = β = = 60°.

Так як OM - бісектриса за властивістю рівнобедренного трикутника, то

∠DOM = ∠MOE = ∠DOE : 2 = 60° : 2 = 30°.OM є висотою, тоді

sin ∠MOE =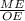 ⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.

cos ∠MOE = ⇒  MO = cos ∠MOE * OE = cos 30° * OE = =

Проведемо відрізок OH - який буде висотою за властивісью шестикутної піраміди.РозглянемоΔ MOH.

cos ∠MOH = cos α =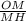  ⇒ MH = .

За властивістю правильної піраміди усі її грані є рівними рівнобедренними трикутниками, отже Δ HDE - рівнобедренний.Проведемо відрізок HM - який є медіаною так як DM = ME, За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, отже .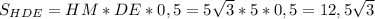

S бічної поверхні = 6 * = .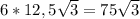