Snlm=6 кв.см.
Объяснение:
Дано:
ΔABC; Sabc=18 кв.см.
M-точка пересечения его медиан.
AE;BL;CF-медианы.
MK║BC
Найти: Snlm-?
1) LEMC=LNMA - по свойству вертикальных углов.
2) LCNA=LNCB - накрест лежащие углы.
3) ΔCME и ΔAMN - подобные по двум углам (первый признак подобия)
4) По свойствам медианы:
Safm=Sfbm=Sbem=Semc=Smlc=Smal⇒Semc=Sabc/6=18/6=3 кв.см.
5) По свойствам медианы: AM/ME=2/1=2
Так как AM и ME подобные стороны ΔCME и ΔAMN, то коэффициент подобия k=AM/ME=2
6) Зная коэффициент подобия, вычислим Samn:
Samn=*Scme=*3=4*3=12 кв.см.
7) Sanc=Sanm+Saml+Slmc=12+3+3=18 кв.см.
8) Медиана-NL делит площадь в ΔANC на две равновеликие части поэтому:
Slnc=Sanc/2=18/2=9 кв.см.
9) Искомая площадь ΔNLM равна:
Snlm=Slnc-Slmc=9-3=6 кв.см.
Задание 1.
(Смотри вложение 1 )
Осевым сечением цилиндра является прямоугольник.
Формула площади прямоугольника: S = a*b , где
а - одна сторона
b - другая сторона
Для нашего прямоугольника высота цилиндра = стороне а, а диаметр ( 2 радиуса) = стороне b. Получается S = 8*26 = 208 см²
Формула площади полной поверхности цилиндра: , где
2πR² - площадь оснований
πRh - площадь боковой поверхности
У нас всё известно ⇒ подставляем значения в формулу
см²
Формула объёма цилиндра: , где
πR² - площадь основания
h - высота
см³
Задание 2.
(Смотри вложение 2 )
Осевым сечением конуса является треугольник.
Формула площади треугольника: , где
а - основание
Для нашего прямоугольника высота конуса = высоте сечения, а диаметр ( 2 радиуса) = основанию . Получается
Формула площади полной поверхности конуса: , где
πRL - площадь боковой поверхности
Формула объёма конуса: , где
С осевого сечения найдём высоту
По т. Пифагора:
Теперь у нас всё известно ⇒ подставляем значения в формулу
Snlm=6 кв.см.
Объяснение:
Дано:
ΔABC; Sabc=18 кв.см.
M-точка пересечения его медиан.
AE;BL;CF-медианы.
MK║BC
Найти: Snlm-?
1) LEMC=LNMA - по свойству вертикальных углов.
2) LCNA=LNCB - накрест лежащие углы.
3) ΔCME и ΔAMN - подобные по двум углам (первый признак подобия)
4) По свойствам медианы:
Safm=Sfbm=Sbem=Semc=Smlc=Smal⇒Semc=Sabc/6=18/6=3 кв.см.
5) По свойствам медианы: AM/ME=2/1=2
Так как AM и ME подобные стороны ΔCME и ΔAMN, то коэффициент подобия k=AM/ME=2
6) Зная коэффициент подобия, вычислим Samn:
Samn=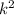
*Scme=
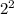*3=4*3=12 кв.см.
7) Sanc=Sanm+Saml+Slmc=12+3+3=18 кв.см.
8) Медиана-NL делит площадь в ΔANC на две равновеликие части поэтому:
Slnc=Sanc/2=18/2=9 кв.см.
9) Искомая площадь ΔNLM равна:
Snlm=Slnc-Slmc=9-3=6 кв.см.
Задание 1.
(Смотри вложение 1 )
Осевым сечением цилиндра является прямоугольник.
Формула площади прямоугольника: S = a*b , где
а - одна сторона
b - другая сторона
Для нашего прямоугольника высота цилиндра = стороне а, а диаметр ( 2 радиуса) = стороне b. Получается S = 8*26 = 208 см²
Формула площади полной поверхности цилиндра: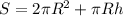
, где
2πR² - площадь оснований
πRh - площадь боковой поверхности
У нас всё известно ⇒ подставляем значения в формулу
Формула объёма цилиндра: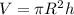
, где
πR² - площадь основания
h - высота
У нас всё известно ⇒ подставляем значения в формулу
Задание 2.
(Смотри вложение 2 )
Осевым сечением конуса является треугольник.
Формула площади треугольника: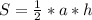
, где
а - основание
h - высота
Для нашего прямоугольника высота конуса = высоте сечения, а диаметр ( 2 радиуса) = основанию . Получается
Формула площади полной поверхности конуса: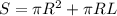
, где
πR² - площадь основания
πRL - площадь боковой поверхности
У нас всё известно ⇒ подставляем значения в формулу
Формула объёма конуса: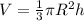
, где
πR² - площадь основания
h - высота
С осевого сечения найдём высоту
По т. Пифагора:
Теперь у нас всё известно ⇒ подставляем значения в формулу