1. Первым шагом нам нужно вспомнить определение равнобедренного треугольника. Равнобедренный треугольник — это треугольник, у которого две стороны равны друг другу.
2. В нашей задаче говорится, что боковые стороны равнобедренного треугольника равны 25. Это означает, что сторона AB и сторона AC имеют одинаковую длину и равны 25.
3. Также в задаче указано, что основание равнобедренного треугольника равно 30. Это означает, что сторона BC имеет длину 30.
4. Мы знаем, что радиус вписанной окружности равнобедренного треугольника проходит через центр окружности и перпендикулярен к основанию треугольника. От центра окружности проведем перпендикуляр к стороне BC и обозначим его точкой D.
5. Так как радиус вписанной окружности и проведенный к стороне BC перпендикуляр неотрывно связаны, то перпендикуляр DB должен быть равной длины с перпендикуляром DC.
6. Поскольку треугольник является равнобедренным, сторона AB равна стороне AC и равна 25. Таким образом, мы можем разделить основание треугольника BC на две равные части, каждая из которых имеет длину 30/2 = 15.
7. Обозначим половину основания BC (то есть отрезок BD или CD) как x. Это означает, что длина BD и CD равна x = 15.
8. Из теоремы Пифагора, мы знаем, что квадрат гипотенузы равен сумме квадратов катетов. Применим эту теорему к прямоугольному треугольнику BCD: BC^2 = BD^2 + CD^2.
9. В нашем случае BC = 30, BD = x = 15 и CD = x = 15. Подставим эти значения в уравнение: 30^2 = 15^2 + 15^2.
12. Как видим, это уравнение неверное. Значит, мы допустили ошибку в предположении, что треугольник является прямоугольным.
13. Таким образом, мы можем сделать вывод, что равнобедренный треугольник не является прямоугольным.
14. Радиус вписанной окружности равнобедренного треугольника можно найти, используя формулу: r = S / p, где r - радиус, S - площадь треугольника, p - полупериметр треугольника.
15. Для того чтобы найти площадь треугольника, нам нужно знать его высоту. Однако, в данной задаче у нас нет информации о высоте треугольника.
16. Поэтому, без дополнительной информации, мы не можем найти радиус вписанной окружности треугольника.
В итоге, ответ на данный вопрос - мы не можем найти радиус вписанной окружности треугольника без дополнительной информации о высоте треугольника или других углах и сторонах.
ответ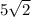
1. Первым шагом нам нужно вспомнить определение равнобедренного треугольника. Равнобедренный треугольник — это треугольник, у которого две стороны равны друг другу.
2. В нашей задаче говорится, что боковые стороны равнобедренного треугольника равны 25. Это означает, что сторона AB и сторона AC имеют одинаковую длину и равны 25.
3. Также в задаче указано, что основание равнобедренного треугольника равно 30. Это означает, что сторона BC имеет длину 30.
4. Мы знаем, что радиус вписанной окружности равнобедренного треугольника проходит через центр окружности и перпендикулярен к основанию треугольника. От центра окружности проведем перпендикуляр к стороне BC и обозначим его точкой D.
5. Так как радиус вписанной окружности и проведенный к стороне BC перпендикуляр неотрывно связаны, то перпендикуляр DB должен быть равной длины с перпендикуляром DC.
6. Поскольку треугольник является равнобедренным, сторона AB равна стороне AC и равна 25. Таким образом, мы можем разделить основание треугольника BC на две равные части, каждая из которых имеет длину 30/2 = 15.
7. Обозначим половину основания BC (то есть отрезок BD или CD) как x. Это означает, что длина BD и CD равна x = 15.
8. Из теоремы Пифагора, мы знаем, что квадрат гипотенузы равен сумме квадратов катетов. Применим эту теорему к прямоугольному треугольнику BCD: BC^2 = BD^2 + CD^2.
9. В нашем случае BC = 30, BD = x = 15 и CD = x = 15. Подставим эти значения в уравнение: 30^2 = 15^2 + 15^2.
10. Выполняя вычисления, получим: 900 = 225 + 225.
11. Кратив, получим: 900 = 450.
12. Как видим, это уравнение неверное. Значит, мы допустили ошибку в предположении, что треугольник является прямоугольным.
13. Таким образом, мы можем сделать вывод, что равнобедренный треугольник не является прямоугольным.
14. Радиус вписанной окружности равнобедренного треугольника можно найти, используя формулу: r = S / p, где r - радиус, S - площадь треугольника, p - полупериметр треугольника.
15. Для того чтобы найти площадь треугольника, нам нужно знать его высоту. Однако, в данной задаче у нас нет информации о высоте треугольника.
16. Поэтому, без дополнительной информации, мы не можем найти радиус вписанной окружности треугольника.
В итоге, ответ на данный вопрос - мы не можем найти радиус вписанной окружности треугольника без дополнительной информации о высоте треугольника или других углах и сторонах.