Большее основание равнобедренной трапеции в 2 раза больше меньшего основания. Расстояние от середины большего основания до вершины тупого угла равно меньшему основанию.
Вычисли периметр трапеции, если длина меньшего основания равна 19 см.
ответ: периметр трапеции равен
см.
2
Анжела измерила два угла параллелограмма и получила углы величиной 54 и 126 градус(-ов, -а).
Верны ли её измерения?
ответ:
(да или нет).
3
Периметр параллелограмма равен 108 м.
Известно, что одна сторона в 5 раз больше другой.
Вычисли стороны параллелограмма.
Меньшая сторона равна
м.
Большая сторона равна
м.
4
В разных сторонах от прямой даны точки A и B на расстояниях 11,3 см и 2,8 см от прямой соответственно.
Определи расстояние серединной точки C отрезка AB до прямой.
ответ: расстояние от точки C до прямой равно
см.
Объяснение:
Объём пирамиды:
Значит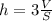
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна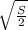
Тогда, по теореме Пифагора:
Проведем две медианы к боковым сторонам треугольника.
Так как он равнобедренный, медианы эти равны и отсекают от исходного треугольника два меньших, равных между собой.
Угол при основании неизвестен, поэтому обозначим его α и его косинус - cosα
Выразим медиану одного из образовавшихся треугольников по теореме косинусов.
Чтобы найти косинус угла при основании, применим теорему косинусов к данному в условии задачи треугольнику, стороны которого известны.
Подставив найденное значение cosα в уравнение медианы, найдем ее длину.