Высота прямоугольного треугольника, проведённая к гипотенузе, равна 13 см, а один из катетов — 26 см. Найдите больший острый угол треугольника. ответ дайте в градусах.
Для решения данной задачи давайте рассуждать логично-
НЕ МОЖЕТ быть правильный многоугольник из данного, если из одну вершину мы соединим , например , с пятой вершиной по часовой стрелке, а против часовой - с шестой. Тогда стороны не тбудут равными. Это дает нам ключ к решению задачи.
Значит, первый многоугольник получается, если мы соединим вершины через одну, т.е. каждую вторую.
1)Получится 60/2=30-угольник.
2)Потом 60/3=20 угольник. И так далее, берем делители числа 60
По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.
Пусть , BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC ⇒ ΔDEC - равнобедренный ⇒
∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.
2∠FBD + 2∠DBE = 360°
2∠FBD + 360° - 2α = 360°
∠FBD = α
Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.
Объяснение:
Для решения данной задачи давайте рассуждать логично-
НЕ МОЖЕТ быть правильный многоугольник из данного, если из одну вершину мы соединим , например , с пятой вершиной по часовой стрелке, а против часовой - с шестой. Тогда стороны не тбудут равными. Это дает нам ключ к решению задачи.
Значит, первый многоугольник получается, если мы соединим вершины через одну, т.е. каждую вторую.
1)Получится 60/2=30-угольник.
2)Потом 60/3=20 угольник. И так далее, берем делители числа 60
3) 60/4=15
4) 60/5=12
5) 60/6=10
6) 60/10=6
7) 60/12=5
8) 60/15=4
9) 60/20=3
Итого - 9 многоугольников
По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.
Пусть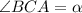
, BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC ⇒ ΔDEC - равнобедренный ⇒
∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.
2∠FBD + 2∠DBE = 360°
2∠FBD + 360° - 2α = 360°
∠FBD = α
Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.