Центрі О нүктесінде болатын шеңбердің LM хордасы радиусқа тең. Осы хордаға перпендикуляр болатын ЕК диаметрі жүргізілген. ЕК диаметрі мен LM хордасы Авс нүктесінде қиылысады. L. A кесіндісінің ұзындығы 12,4 см.

а) есептің шарты бойынша суретін салыңыз;

b) LM хордасының ұзындығын табыңыз;

c) ЕК диаметрінің ұзындығын табыңыз;

d) OLM үшбұрышының периметрін табыңыз.
​

Сторона більшого квадрата - 15 см

Площа більшого квадрата - 225 см²

Периметр більшого квадрата більше за периметр меншого в 5 разів.

Объяснение:

Сторона меншого квадрата - х см. Сторона більшого квадрата - 5х. Площа меншого квадрата - х² = 9 см². Площа більшого квадрата - (5х)². Периметр меншого квадрата - 4х. Периметр більшого квадарата - 4(5х).

З цього бачимо, що сторона (х) меншого квадрата дорівнює √9, тобто 3 см.

Тоді сторона більшого квадрата дорівнює 3 · 5 = 15 (см).

З цього площа більшого квадрата - 15² = 225 (см²)

Периметр меншого квадрата: 3 · 4 = 12 (см)

Периметр більшого квадрата: 15 · 4 = 60 (см).

Периметр більшого квадрата більше за периметр меншого в: 60 : 12 = 5 (разів)

Сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см от нее и является квадратом. Площадь боковой поверхности цилиндра равна 8√3π см2 . Найдите площадь сечения.

Объяснение:

S( бок цилиндра)=2πrh, где , r — радиус основания цилиндра, h — высота цилиндра. Тогда  8√3π=2πrh или 4√3=rh  . Возведем обе части в квадрат( зачем? пригодится) (4√3)²=r²h ² , 48=r²h² (*) .

В сечении -квадрат АВСК. Причем АВ=BC=h.  Площадь сечения S(квадрата)=BC²=h².Используя (*) h²=S=48:r²  .

 Т.к. сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см , то ОМ⊥ВС , ОМ=2 см.

ΔВСО-равнобедренный и ОМ-высота , а значит медиана . Тогда

ВМ=  .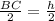

ΔВМО-прямоугольный по т. Пифагора r²=2²+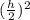  или

 r²=4+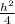  или r²=  .

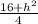S=48 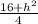 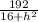:  =    (см²)