Через дві твірні конуса проведено площину, яка нахилена до основи під кутом ∠ α. Ця площина перетинає основу конуса по хорді, яку видно з центра основи під ∠ β.
Знайдіть площу бічної поверхні конуса,якщо його твірна дорівнює m
На русском :
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом ∠ α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под ∠ β.
Найдите площадь боковой поверхности конуса, если его образующая равна m
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
4) ΔMHO- прямоугольный :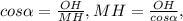 или
или 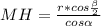 .
.
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
r =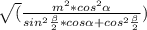 =
= 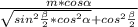 .
.
6) S(бок.конуса )= π *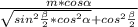 *m
*m
S(бок.конуса )=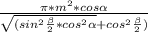 ( ед²) .
( ед²) .