Через две образующих конуса, угол между которыми равен α, проведена плоскость, пересекающая основание конуса по хорде, которую видно из центра основания под углом β. Радиус основания конуса равен R. Найдите: 1) площадь сечения; 2) длину образующей конуса.

Показать ответ

Ответ:

wereweek777

14.02.2022 21:07

$\boxed{AB = AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}}$

$\boxed{S_{зCAB} = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}}$

Объяснение:

Дано: OC = OB = R, ∠BOC = β, ∠BAC = α, O - центр окружности в основании конуса

Найти: AC,BC,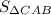 $S_{зCAB}$ - ?

Решение: Пусть точка M - середина отрезка CB. Рассмотрим треугольник ΔCOB. Треугольник ΔCOB - равнобедренный, так как по условию OC = OB = R. Проведем отрезок OM. Так как по построению CM = MB, то по определению MO - медиана равнобедренного треугольника ΔCOB. Так как CB - основание треугольника ΔCOB

(по условию OC = OB = R), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда ∠COM = ∠BOM = ∠BOC : 2 = β : 2 = 0,5β. Так как OM - высота, то треугольник ΔMOB - прямоугольный. Рассмотрим треугольник ΔMOB.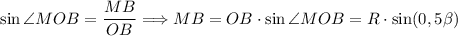 $\sin \angle MOB = \dfrac{MB}{OB} \Longrightarrow MB = OB \cdot \sin \angle MOB = R \cdot \sin (0,5\beta )$ .

Рассмотрим треугольник ΔCAB. Треугольник ΔCAB - равнобедренный, так как по условию AC = AB как образующие конуса. Проведем отрезок AM. Так как по построению CM = MB, то по определению MA - медиана равнобедренного треугольника ΔCAB. Так как CB - основание треугольника ΔCAB (AC = AB как образующие конуса), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда

∠CAM = ∠BAM = ∠BAC : 2 = α : 2 = 0,5α. Так как AM - высота, то треугольник ΔMAB - прямоугольный. Рассмотрим треугольник ΔMAB.

$\sin \angle MAB = \dfrac{MB}{AB} \Longrightarrow AB = \dfrac{MB}{\sin \angle MAB} = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$ .

Так как AC = AB как образующие, то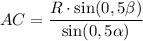 $AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$ .

По формуле площади для треугольника ΔBAC:

$S_{зCAB} = 0,5 \cdot AC \cdot AB \cdot \sin \angle BAC = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}$ .