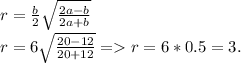Через сторону АВ равностороннего треугольника АВС проведена плоскость α. Проекция точки С на эту плоскость удалена от прямой АВ на расстояние 2 см. АС = 8 см. Найдите: 1) расстояние от точки С до плоскости α; 2) длины проекций сторон данного треугольника на плоскость α.
Формула вычисления стороны, зная 2 другие, и угол между ними:
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова:
Формула вычисления вписанной окружности около равнобёдренного треугольника такова:
см. АС = 8 см. Найдите: 1) расстояние от точки С до плоскости α;
АВСД - трапеция , АВ=СД=37 см , ВС=13 см , ВД - биссектриса ∠В .
Так как ВД - биссектриса ∠В , то ∠АВД=∠СВД .
Так как ВС║АД и ВД - секущая, то ∠СВД=∠АДВ как внутренние накрест лежащие углы, и тогда ∠АВД=∠АДВ ⇒ ΔАВД - равнобедренный, АВ=ВД=37 см .
Проведём ВН⊥АД и СМ⊥АД . ВСМН - прямоугольник и МН=ВС=13 см
АН=МД=37-13=24 см , АН=МД=24:2=12 см .
Рассмотрим ΔАВН .
По теореме Пифагора ВН=√(АВ²-АН²)=√(37²-12²)=√1225=35 см .
ВН - высота трапеции.
Площадь трапеции:
S=(АД+BC)/2*ВН=(37+13)/2*35=50/2*35=25*35=875 см²
1)
1. E
2. F
3. B
4. E
5. A
6. D.
Теорема косинусов: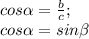
Теорема синусов: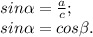
3)
Формула вычисления стороны, зная 2 другие, и угол между ними:
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова: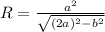
Формула вычисления вписанной окружности около равнобёдренного треугольника такова: