Через точки a и b проведены прямые перпендикулярные плоскости альфа пересекающие ее в точках A1 и B1 соответственно. Найдите расстояние между точками A1 и B1, если AB=32, BB1=11, AA1=29 и отрезок не пересекает альфу

Показать ответ

Ответ:

km546729

14.08.2022 22:40

Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.

Объяснение:

Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК= $\frac{\beta }{2}$ .

ΔАОК- прямоугольный ,

cos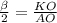 $\frac{\beta }{2} =\frac{KO}{AO}$ , KO=R*cos $\frac{\beta }{2}$ ;

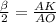sin $\frac{\beta }{2} =\frac{AK}{AO}$ ,AK=R*sin $\frac{\beta }{2}$ ,AB=α2Rsin $\frac{\beta }{2}$ .

ΔSKO прямоугольный ,cos α=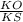 $\frac{KO}{KS}$ , KS=R*cos $\frac{\beta }{2}$ /cosα.

S=0,5*AB*SK ,S=0,5*2R*sin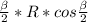 $\frac{\beta }{2} *R*cos\frac{\beta }{2}$ / cosα,

S=0,5*R²*sinβ/cosα=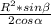 $\frac{R^{2} *sin\beta }{2 cos\alpha }$

0,0(0 оценок)

Ответ:

sveta17032001

01.07.2021 02:13

на фото ответ

Объяснение:

второе задание:

1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то

<MNE = <CDE = 68°

2. Зная, что развернутый угол равен 180°, находим угол DNM:

<DNM = 180 - <MNE = 180 - 68 = 112°

3. Поскольку DM - биссектриса, то угол MDN = <CDE : 2 = 68 : 2 = 34°

4. Зная два угла треугольника DMN, находим неизвестный угол:

<DMN = 180 - <MDN - <DNM = 180 - 34 - 112 = 34°