Через точку К, лежащую между параллельными плоскостями Альфа и бэта проведены две прямые a и b, где альфа пересекает бету в точке А1. Прямая а пересекает плоскость бета в точке А2, прямая б пересекает плоскость бета в точке Б1 и Б2 ​

12 см

Объяснение:

1) Острый угол, составляющий 2/3 прямого угла, равен:

90 · 2/3 = 60°.

2) Второй острый угол прямоугольного треугольника равен:

180 - 90 - 60 = 30°.

3) Меньший катет лежит против меньшего угла, то есть против угла 30°.

Катет, лежащий против угла 30°, равен половине гипотенузы.

Пусть х - меньший катет прямоугольного треугольника, тогда гипотенуза равна 2х. Составим уравнение и найдём х:

х + 2х = 18

3х = 18

х = 18 : 3 = 6 см - это длина меньшего катета.

4) Находим длину гипотенузы:

6 · 2 = 12 см

ответ: 12 см

В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.

S(осн.)=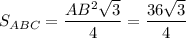 =9√3 см².

Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.

=√3 см

В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.

=√147 см

Боковые грани правильной пирамиды это равные треугольники.

S(бок.)=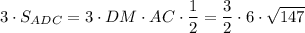 =9√147 см²

S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²

ответ: 9√3 + 9√147 см².