Через точку k, не лежащую между параллельными плоскостями α и β, проведены прямые a и b. прямая a пересекает плоскости α и β в точках a1 и a2 соответственно, b - в точках b1 и b2. найти kb2, если a1b1 : a2b2 = 5 : 3, kb1 = 5см.
Проведём через вершины B & C — радиусы: BO == CO = r.
AO == OD = AD/2 = r (половина диаметра равна радиусу окружности).
Наши треугольники таковы: ΔAOB; ΔBOC; ΔCOD.
Учитывая информацию, данную нам задачей, и новые отрезки — найденные нами, мы составим определения: (AO == OD == OC == BO); (AB == BC == CD).
И так как каждый треугольник — имеет одну пару равных друг другу сторон (каждые 2 стороны в каждом треугольнике — радиусы), и равные основания (AB == BC ==CD), то по третъему признаку равенства треугольников: ΔAOB == ΔBOC == ΔCOD.
Что и означает, что: <AOB == <BOC == <COD ⇒ <COD == <BOC = 180/3 = 60°.
<BOD = <COD + <BOC = 60°+60° = 120°.
Вывод: <BOD = 120°.
2)
1.
Отрезки OA & OB — радиусы, так как каждый из них проведён с одной точки, находящийся на окружности, до её центра.
CO == OB = r.
<COB = 60° ⇒ <AOB = 180-60 = 120° (так как <AOB & <COB — смежные углы).
<AOB = 120°; OA == OB ⇒ <B == <AOB.
<AOB = (180° - <OAB)/2 = 30°.
AD — касательная, что и означает, что радиус, проведённый с точки касания до центра окружности — перпендикулярен этой касательной.
треугольник, а треугольник - описанным около этой окружности.
Теорема. В любой треугольник можно вписать окружность и при этом только одну.
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность.
Теорема. Около любого треугольника можно описать окружность и при этом только одну.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
1)
AB == BC == CD.
Проведём через вершины B & C — радиусы: BO == CO = r.
AO == OD = AD/2 = r (половина диаметра равна радиусу окружности).
Наши треугольники таковы: ΔAOB; ΔBOC; ΔCOD.
Учитывая информацию, данную нам задачей, и новые отрезки — найденные нами, мы составим определения: (AO == OD == OC == BO); (AB == BC == CD).
И так как каждый треугольник — имеет одну пару равных друг другу сторон (каждые 2 стороны в каждом треугольнике — радиусы), и равные основания (AB == BC ==CD), то по третъему признаку равенства треугольников: ΔAOB == ΔBOC == ΔCOD.
Что и означает, что: <AOB == <BOC == <COD ⇒ <COD == <BOC = 180/3 = 60°.
<BOD = <COD + <BOC = 60°+60° = 120°.
Вывод: <BOD = 120°.
2)
1.
Отрезки OA & OB — радиусы, так как каждый из них проведён с одной точки, находящийся на окружности, до её центра.
CO == OB = r.
<COB = 60° ⇒ <AOB = 180-60 = 120° (так как <AOB & <COB — смежные углы).
<AOB = 120°; OA == OB ⇒ <B == <AOB.
<AOB = (180° - <OAB)/2 = 30°.
AD — касательная, что и означает, что радиус, проведённый с точки касания до центра окружности — перпендикулярен этой касательной.
То есть: <OAD = 90°; <OAB = 30° ⇒ <DAB = 90-30 = 60°.
Вывод: <DAB = 60°.
2.
Проведём отрезки AO & OD.
AO == OD == CO == OB = r.
Эти треугольники равны по трём сторонам (третий признак равенства треугольников).
Тоесть: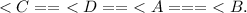
Как мы видим — накрест лежащие углы равны: <C == <B.
А первый признак параллельности прямых таков: если накрест лежащие углы друг другу равны, то: a║b.
Тоесть: AB║CD.
треугольник, а треугольник - описанным около этой окружности.
Теорема. В любой треугольник можно вписать окружность и при этом только одну.
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность.
Теорема. Около любого треугольника можно описать окружность и при этом только одну.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.