Через вершину В правильного треугольника АВС со стороной 6см, проведено прямую МВ, перпендикулярную к плоскости треугольника. Расстояние от точки М к прямой АС равно 2√13 см. Найдите расстояние от точки М к плоскости АВС
1)В основании правильной четырёхугольной пирамиды лежит квадрат, а у квадрата все стороны равны, что говорить о том, что
2)Зная что диагональ равна , найдём .
Поскольку диагонали квадрата в точке их пересечения делятся пополам, найдём .
3)Рассмотрим треугольник , по рисунку видно, что он прямоугольный, поскольку высота из вершины S к плоскости основания. Тогда по теореме Пифагора наёдем высоту.
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3;4,считая от вершины угла при основании треугольника.Найдите боковую сторону треугольника,если его основание равно 12 см.
Пусть К, М, Р- точки касания соответственно сторн АВ,ВС,АС.
Пусть одна часть х см, тогда Ак=3х, КВ=4х.
Т.к треугольник равнобедренный , то СМ=3х,
По свойству отрезков касательных АК=АР=3х, СМ=СР=3х.
Дано:
Найти: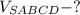
1)В основании правильной четырёхугольной пирамиды лежит квадрат, а у квадрата все стороны равны, что говорить о том, что
2)Зная что диагональ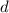 равна
равна 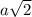 , найдём
, найдём 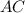 .
.
Поскольку диагонали квадрата в точке их пересечения делятся пополам, найдём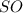 .
.
3)Рассмотрим треугольник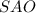 , по рисунку видно, что он прямоугольный, поскольку
, по рисунку видно, что он прямоугольный, поскольку 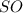 высота из вершины S к плоскости основания. Тогда по теореме Пифагора наёдем высоту.
высота из вершины S к плоскости основания. Тогда по теореме Пифагора наёдем высоту.
4)Теперь можно найти объем пирамиды по формуле
ответ: Объем пирамиды равен 640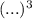
Объяснение:
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3;4,считая от вершины угла при основании треугольника.Найдите боковую сторону треугольника,если его основание равно 12 см.
Пусть К, М, Р- точки касания соответственно сторн АВ,ВС,АС.
Пусть одна часть х см, тогда Ак=3х, КВ=4х.
Т.к треугольник равнобедренный , то СМ=3х,
По свойству отрезков касательных АК=АР=3х, СМ=СР=3х.
АС=3х+3х=6х и АС=12 см ⇒ значит 6х=12, х=2
АВ=3х+4х =7х ,
АВ=14 см