Четырёхугольник ABCD задан координатами своих вершин A (2; 5), B (–3; 7), C (–6; 2), D (–1; –1). Выполните построения и укажите координаты вершин четырёхугольника A1B1C1D1, полученного путём параллельного переноса на вектор {3,-2} из четырёхугольника ABCD.
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
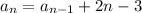, где n - число лучей кратное 3.
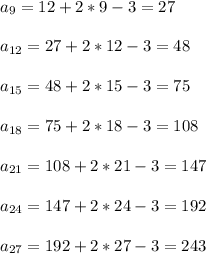
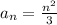
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле:
Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта:
По этой формуле можно считать для любого количества лучей, кратное трём.
1. Найдем координаты векторов АВ, АС, АД, везде, где речь идет о векторах, над ними ставьте черту или стрелку. Но у меня к сожалению нет такой возможности. Чтобы найти их координаты, надо от координат конца вычесть координаты начала вектора, АВ(-2-3; 1-2;3-4); АВ(-5;-1;-1)
АС(-1;-4;-5); АД(-1;3;-) Объем найдем, как 1/6 от модуля детерминанта или определителя, где в первой строке поставим координаты вектора АВ, во второй АС , в третьей АД, и вычислим этот определитель по правилу треугольника.
v=(1/6)*║-5 -1 -1 ║
║-1 -4 -5║
║ -1 3 1║, здесь линии должны быть непрерывными, как в модуле, а раскрывается этот определитель так
(1/6)*(модуль от (20-5+3+4-1-75))= модуль минус 54/6=9, т.е. объем равен
9 ед. куб. Из формулы объема пирамиды, известного из курса средней школы, v=s*h/3, находим высоту h=3v/s=3*9/15.3=9/5.1=30/17≈1.76