Чому дорівнює менша сторона паралелограма, якщо вона на 7 см менша від іншої сторони,а периметр дорівнює 46см.

Ответ: 6 см

Объяснение:   Угол между плоскостями — это угол между перпендикулярами,  проведенными в этих плоскостях  к одной точке на линии их пересечения.

  Линия пересечения - прямая СА, перпендикуляры к ней НВ и НК. Угол ВНК=30°(дано)

  ВН - высота ∆ АВС к стороне АС. Площадь ∆ АВС по формуле Герона равна 24 см².

Из формулы площади треугольника высота ВН=2Ѕ:АС=48:4=12 (см).

  Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из  той точки на плоскость.

Из прямоугольного ∆ ВКН искомое расстояние ВК=ВН•sin30°=12•1/2=6 см

32 cм²

Объяснение:

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:

Sбок= 1/2*(Р1+Р2)*L,

где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)

Найдём сто­роны оснований правильной четырехугольной усеченной пирамиды.

Диагональ квадрата: d = a√2, где а  - сторона квадрата.

⇒ а = d/√2

АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.

Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.

Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.

Найдем апофему L

Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.

Т.к. r=a /2 (половина стороны основания), то  

О1М1= А1Д1/2 =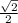  

ОМ = АД/2 =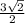  

Опустим перпендикуляр М1К из точки М1 верхнего основания  на нижнее основание. Получим прямоугольный ΔМ1КМ.

Т.к. М1К⊥КМ, КМ⊥ДС,  то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).

КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1=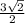   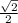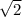- = см.

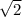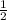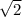Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° = : = 2 cм

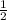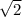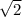Sбок = * ( 12 + 4 ) * 2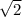 = 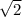(12+4) 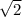= 2*16=32 cм²