CРОЧНО іть висоту рівностороннього трикутника, якщо радіус кола, описаного навколо цього трикутника, дорівнює 12 см.

9 см
18 см
6 см
12 см
Питання №2 ?

Бічна сторона рівнобедреного трикутника ділиться точкою дотику кола у відношенні 2 : 3, рахуючи віл вершини кута при основі трикутника. Знайдіть основу трикутника, якщо його бічна сторона дорівнює 15 см.

18 см
6 см
12 см
15 см
Питання №3 ?

У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки 3 см і 10 см. Знайдіть радіус кола, якщо периметр трикутника дорівнює 30 см.

4 см
6 см
5 см
2 см
Питання №4 ?

До кола, вписаного в рівнобедрений трикутник АВС, проведено дотичну, яка перетинає бічні сторони АВ і АС у точках М і К відповідно. Знайдіть периметр трикутника АВС, якщо периметр трикутника АМК дорівнює 14 см і АВ = АС = 10 см.

26 см
28 см
32 см
24 см
Питання №5 ?

Коло, вписане в трикутник АВС, дотикається до сторони АВ у точці D. Знайдіть сторону ВС, якщо AD = 3 см, а периметр трикутника АВС дорівнює 22 см.

8 см
12 см
10 см
14 см
Питання №6 ?


На рисунку точка O – центр вписаного кола, AB=BC. Знайдіть кут ABO.

Треугольник с прямым углом - это прямоугольный треугольник.

Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.

Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).

Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).

Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.

То есть -

h = 4,8 см.

Решение с ответом:

AB = 12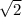 см

BC = 20 см

A = 45 градусов

BM - h

------------------------

СМ = ? см

Высота BM является перпендикуляром, опущенным на AC.

Т.е угол BMA и угол BMC - прямоугольные ( 90 градусов)

расс-им прямоугольный треугольник ABM:

угол BAM = 45 градусов (из условия)

угол  BMA = 90 градусов (BM - высота)

Найдем угол ABM по Теореме о сумме углов треугольника:

180 - (BAM + BMA) = 180 - (90 + 45) = 45 градусов.

Прямоугольный треугольник ABM является равнобедренным, его катеты равны м-у собой.

AM = BM

Гипотенуза у треугольника - AB, она равна 12 корень из 2 ()

Из Теоремы Пифагора (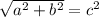) выходит, что квадрат равных м-у собой катетов a и b равен 144, корень из 144 - 12.

т.е AM = BM = 12 см.

расс-им треугольник BMC:

угол BMC - также прямоугольный.

BM = 12 см (по решению)

BC = 20 cм (из условия)

Катет CM = ?  см

Найдем его из Обратной Теоремы пифагора:

см

ОТРЕЗОК CM РАВЕН 16 СМ.