Поэтому, как только начинаешь читать следы какого-нибудь одного существа, глядишь, а ты уже разбираешься в жизни сотен и тысяч других существ будь то звери птицы или даже растения. интересное это дело - читать следы. но самое интересное в этом то, что сколько бы ты ни читал их, до конца их ни как не прочитаешь.это от того, что следовую книгу пишет сама жизнь, которая идет все время вперед и никогда не останавливается, а следы, как и подобает , хотя и идут за жизнью, но остаются у нее позади. всем интересно читать эту следовую книгу и всем от этого бывает польза. только читать ее нужно строчка за строчкой, как на охоте, надо обязательно глядеть вперед, по направлению следов, тогда не ошибешься и заранее будешь знать, что надо делать в будущем.
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б)
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
1. Могут.
2. б) 6 см
3. б) 45°
Объяснение:
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б)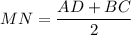
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
а) ВС лежит в плоскости (АВС),
МА пересекает (АВС) в точке А,
А не лежит на прямой ВС, значит
МА и ВС скрещивающиеся.
б) ∠(МА, AD) = 45° по условию,
BC║AD, значит
∠(МА, ВС) = 45°