Дан параллелограмм ABCD и не пересекающая его плоскость альфа. Из вер- шин параллелограмма проведены параллельные прямые, которые пере-
секают плоскость альфа в точках A1, B1, C1, D1. Найдите длину отрезка DD1,
если AA1 = 3 см, BB1 = 4 см, CC1 = 7 см.
1) Пусть сторона основания равнобедренного треугольника равна х см, тогда боковые стороны равны (x+10) см. Зная, что периметр равнобедренного треугольника равен 98 см, составим уравнение
x + 2(x+10) = 98
x + 2x + 20 = 98
3x = 78
x = 26 см - сторона основания
Боковые стороны равнобедренного треугольника 26 + 10 = 36 см.
2) Теперь примем за х боковую сторону равнобедренного треугольника, тогда сторона основания равна (x+10) см. Составим уравнение
x + 10 + 2x = 98
3x = 88
x = 88/3 см - боковая сторона
88/3 + 10 = 118/3 см - сторона основания
Т.е. у обеих вариантов выполняется неравенство треугольника, значит данная задача имеет два решения.
ответ: 26 см, 36 см, 36 см или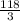 см,
см, 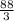 см,
см, 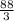 см.
см.
Для построения серединного перпендикуляра надо:
построить две окружности - с центром в точке А и с центром в точке С, произвольного радиуса, но больше половины длины отрезка АС;
у этих окружностей найти точки пересечения - К и М;
Через точки пересечения окружностей провести прямую а.
Эта прямая - серединный перпендикуляр.
Затем этот серединный перпендикуляр надо продлить до пересечения со стороной ВС. Точка пересечения серединного перпендикуляра и стороны ВС - искомая точка (на чертеже это точка О).
Обратите внимание, в зависимости от треугольника задача может и не иметь решение. На первом чертеже точка О лежит на стороне ВС - задача имеет решение, на втором чертеже точка О не лежит на стороне ВС, а находится на продолжении этой стороны, на третьем такую точку совсем не построить.
В этой задаче необходимо провести исследование и выяснить, когда задача имеет решение.