дан прямоугольник АВСД со сторонами 7см. и 24см. и построены точки А1 и С1 симметричные точкам А и С относительно прямой ВД.докажите что АА1 СС1 прямоугольник и найдите его диагональ А1 С1

Показать ответ

Ответ:

AnnaMarkeca91

22.09.2022 13:08

1. 6+9+10= 25 см 2. 25×2= 50 см ответ: 50 см периметр треугольника

2. Средняя линия = 1/2 сумме оснований. т. к. основания относятся как к 3:5, можно принять, что они равны 3х и 5х, т. е. полсуммы основания равна 4х = 32 см, отсюда х = 8 см. основания: 3*8 = 24 см и 5*8 = 40 см.

3. P=2* (7+12)=2*19=38 (см). ответ: 38 см.

4. Р=3+7+2m=10+10=20. ответ:20.

5. Дано: <АДВ=43, <АСД=37 <САД=22

Решение: в вписанном 4-х угольнике суммы противоположных углов= 180 гр. угол DAC вписанный и равен половине дуги, на которую опирается, значит дуга DC=44 гр. дуга AD=37*2=74 гр. дуга AB=43*2=86 гр., тогда дуга BC = 360-(86+44+74)=360-204=156 ответ: 156

0,0(0 оценок)

Ответ:

dariagumennik

10.05.2021 21:18

Відповідь:

1) 6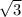 $\sqrt{3}$ см4 2) 18 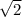$\sqrt{2}$ см; 3)MN=12 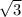$\sqrt{3}$ (см); 4.12√3(см); 5. ∠1=30°, ∠2= 60°, катет= 12√3 см; 6. 64/√3≈37.6 cм; 7. 20/√3≈11,5 см 8. 4 см і 4√3 см.

Пояснення: с- гіпотенуза, а і b- катети

1.Інший кут(протилежний до заданого)катета=180°-(90°+30°)=60° за теоремою синусів прилеглий катет а =12*sin 60°=12*√3/2=6 √3(см)

2. коли кут = 45°, то інший кут теж рівен 45°- трикутник рівнобедрений,

с²=2а².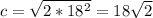 $c=\sqrt{2*18^2}=18\sqrt{2}$ (см)

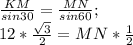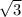3. за теоремою синусів : $\frac{KM}{sin 30}=\frac{MN}{sin 60}; \\ 12*\frac{\sqrt{3} }{2}=MN*\frac{1}{2}$ /*2

MN=12 $\sqrt{3}$ (см)

4. як у першій задачі катет=24*sin 60°=24*√3/2=12√3(см)

5. якщо у прямокутному Δ, катет= 1/2 гіпотенузи, то це катет, що лежить проти кута в 30°.

відповідь: ∠1=30°, ∠2= 60°, катет= 12√3 см.

6. За властивостями ромба : його діагоналі є бісектрисами кутів, у точці перетину ділять себе навпіл, та є перпендикулярні одна до другої. Так як один з кутів 120°, то поділений діагоналю навпіл= 120°:2=60°., трикутник утворений цією діагоналлю буде рівностороннім, так як протилежні кути в ромбу рівні, а сума усіх кутів Δ=60°. Друга напівдіогональбуде висотою цього трикутника( бо діагоналі утворюють між собою прямий кут) Знайдемо сторону ромбу , с²=8²+(с/2)²

4с²-с²=64*4; 3с²=256.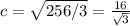 $c= \sqrt{256/3} =\frac{16}{\sqrt{3} }$

P=4*16/√3=64/√3≈37.6 cм

7. за теоремою Піфагору знайдемо сторону в утвореному висотою прямокутному трикутнику с²=10²+ (с/2)²;3с²=400. с= √( 400/3)=20/√3≈11,5 см

8. Діагоналі ромба ділять його на 4-ри прямокутних трикутники, які попарно рівні. Так як діагоналі ромба є його бісектрисами,то утворені трикутники мають кути 30°,60°,90°. тоді менша гіпотинуза = 2*2= 4см, а більша 2√3*2=4√3 см

0,0(0 оценок)

Популярные вопросы: Геометрия