Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
Чертеж прилагается. A - центр окружности. Отметим, что треугольник BCD - прямоугольный, так как угол CBD опирается на диаметр. Далее, известно, что хорда BK перпендикулярна диаметру CD. Пусть H - точка пересечения хорды и диаметра. Получается, что BH - высота в прямоугольном треугольнике, проведенная из вершины прямого угла (хотя это не так важно окажется). Также известно, хорда делится этим самым диаметром пополам. Это следует из того, что треугольник BAK - равнобедренный, так как AK=AB (радиусы), а AH - высота, проведенная к основанию (в смысле не к боковой стороне), но значит и медиана тоже. Тогда BH = 1/2 * BK = 12. Треугольник BHA - прямоугольный, по теореме Пифагора
CH = AC - AH =
HD = AD + AH =
Теперь лишь из прямоугольных треугольников BHC и BHD по теореме Пифагора нужно найти BC и BD соответственно.
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть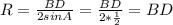
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
Теперь по теореме Пифагора ищем BD
ответ: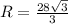
Чертеж прилагается. A - центр окружности. Отметим, что треугольник BCD - прямоугольный, так как угол CBD опирается на диаметр. Далее, известно, что хорда BK перпендикулярна диаметру CD. Пусть H - точка пересечения хорды и диаметра. Получается, что BH - высота в прямоугольном треугольнике, проведенная из вершины прямого угла (хотя это не так важно окажется). Также известно, хорда делится этим самым диаметром пополам. Это следует из того, что треугольник BAK - равнобедренный, так как AK=AB (радиусы), а AH - высота, проведенная к основанию (в смысле не к боковой стороне), но значит и медиана тоже. Тогда BH = 1/2 * BK = 12. Треугольник BHA - прямоугольный, по теореме Пифагора
CH = AC - AH =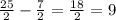
HD = AD + AH =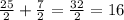
Теперь лишь из прямоугольных треугольников BHC и BHD по теореме Пифагора нужно найти BC и BD соответственно.
ответ: 15 и 20.