Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:
см
см
Площа прямокутного трикутника знаходится як півдобуток його катетів:
см²
Другий б
Висота прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
см
Площа будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти , що до неї проведена:
Возьмем две точки , лежащие на исходной прямой. Пусть это точка (0;6) и (2;4). Построим точки, симметричные данным относительно точки А(1;-2), для этого учтем А будет серединой отрезка, соединяющего точку (о;6) с ей симметричной точкой (х₁;у₁).
(0+х₁)/2=1, откуда х₁= 2
(6+у₁)/2= -2, откуда у₁=-10, Получили точку (2;-10) симметричную точке (0;6) относительно точки А(1;-2).
Аналогично найдем еще одну искомой прямой. Пусть это будет точка
(х₂;у₂), которая симметрична точке (2;4) относительно А(1;-2)
(2+х₂)/2=1; откуда х₂=0
(4+у₂)/2=-2; откуда у₂=-8
получили еще одну точку (0;-8), симметричную точке (2;4) относительно точки А(1;-2)
Составим теперь уравнение прямой, проходящих через найденные точки (2;-10) и (0;-8)
у = кх +в, подставим в это уравнение прямой сначала одну, потом другую точку, получим систему двух уравнений. ИЗ НЕЕ НАЙДЕМ К И В. И отыщем искомую прямую.
2к+в=-10
0*к+в=-8 из второго уравнения в =-8, тогда из первого 2к=-2, к = -1, искомое уравнение прямой примет вид у = -х-8
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
Площа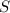 прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
Другий б
Висота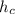 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
Площа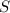 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 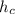 , що до неї проведена:
, що до неї проведена:
Відповідь: 180 см².
Возьмем две точки , лежащие на исходной прямой. Пусть это точка (0;6) и (2;4). Построим точки, симметричные данным относительно точки А(1;-2), для этого учтем А будет серединой отрезка, соединяющего точку (о;6) с ей симметричной точкой (х₁;у₁).
(0+х₁)/2=1, откуда х₁= 2
(6+у₁)/2= -2, откуда у₁=-10, Получили точку (2;-10) симметричную точке (0;6) относительно точки А(1;-2).
Аналогично найдем еще одну искомой прямой. Пусть это будет точка
(х₂;у₂), которая симметрична точке (2;4) относительно А(1;-2)
(2+х₂)/2=1; откуда х₂=0
(4+у₂)/2=-2; откуда у₂=-8
получили еще одну точку (0;-8), симметричную точке (2;4) относительно точки А(1;-2)
Составим теперь уравнение прямой, проходящих через найденные точки (2;-10) и (0;-8)
у = кх +в, подставим в это уравнение прямой сначала одну, потом другую точку, получим систему двух уравнений. ИЗ НЕЕ НАЙДЕМ К И В. И отыщем искомую прямую.
2к+в=-10
0*к+в=-8 из второго уравнения в =-8, тогда из первого 2к=-2, к = -1, искомое уравнение прямой примет вид у = -х-8
ответ у = -х-8