По условию ΔADC равнобедренный с основанием CD, значит углы при основании равны, обозначим их х.
ΔВЕС так же равнобедренный с основанием СЕ, значит углы при основании равны, обозначим их у.
Сумма углов треугольника равна 180°, значит
∠А = 180° - 2х
∠В = 180° - 2у
∠А + ∠В = 180°, так как он односторонние при пересечении параллельных прямых AD и ВЕ секущей АВ. Тогда
(180° - 2x) + (180° - 2y) = 180°
2x + 2y = 180°
x + y = 90°
Угол АСВ развернутый, равен 180°.
∠DEC = 180° - (х + у) = 180° - 90° = 90°
Значит DC⊥CE
; .
Объяснение:
Определим основания трапеции.
Допустим, - основания трапеции.
По свойству трапеции,
- односторонние, при пересечении секущей
Однако а не
никак не могут быть основаниями данной трапеции.
Значит - основания трапеции.
По условию ΔADC равнобедренный с основанием CD, значит углы при основании равны, обозначим их х.
ΔВЕС так же равнобедренный с основанием СЕ, значит углы при основании равны, обозначим их у.
Сумма углов треугольника равна 180°, значит
∠А = 180° - 2х
∠В = 180° - 2у
∠А + ∠В = 180°, так как он односторонние при пересечении параллельных прямых AD и ВЕ секущей АВ. Тогда
(180° - 2x) + (180° - 2y) = 180°
2x + 2y = 180°
x + y = 90°
Угол АСВ развернутый, равен 180°.
∠DEC = 180° - (х + у) = 180° - 90° = 90°
Значит DC⊥CE
Объяснение:
Определим основания трапеции.
Допустим,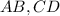 - основания трапеции.
- основания трапеции.
По свойству трапеции,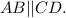
При пересечении двух параллельных прямых секущей, сумма односторонних углов равнаОднако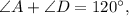 а не
а не 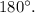
Значит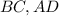 - основания трапеции.
- основания трапеции.
По свойству трапеции,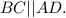
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна