Дан треугольник abc c = 90 °, b = 30 °, ac = 10 см. Точка m перпендикулярна плоскости треугольника ma и нанесены наклоны mc и mb. если amc = 45 °, найти расстояние от точки M до стены BC

Прямые АВ и CD не параллельные, то есть пересекающиеся.

                                                                                                    Дано:  угол ABC =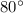 

                                                                                                    угол BCD =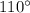 

                                                                                                  _____________________

                                                                                                   Д-ть АВ не параллельно CD

                                                    Решение

1) Предположим, что прямые АВ и СD параллельны. Тогда угол АВС = углу BCD =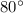  (как при параллельных прямых АВ и CD  и секущей BC)

2) Так как сумма углов в треугольнике равна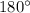  (по теореме о сумме углов в треугольнике), мы приходим к противоречию с первым пунктом моего решения так как угол СВD и угол ВСD в сумме уже дают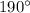 

3) Мы пришли к противоречию, значит наше предположение не верно, и значит прямая АВ не параллельна CD. Ч.т.д.

1). Треугольник NAB - равнобедренный, так как AB=NB;

2). угол ANB = углу NAB ( по свойсвтву равнобедренного треугольника - углы при основании равны);

3). угол MNA = углу ANB (Так как NA-биссектриса треугольника MNP)

4).  угол ANB = угол MNP : 2 (Так как NA биссектриса треугольника MNP)

  угол ANB = 64: 2 = 32 градуса

5).  угол ANB = углу NAB = угол = MNA = 32 градусам ( из доказанного)

 6). Из доказанного следует, что углу NAB = угол = MNA = 32 градусам, а углы NAB и MNA - накрест лежащие при пересечении прямых MN и AB и секущей NA. Следовательно MN||AB