Дана четырёхугольная пирамида SABCD с прямоугольником ABCD в основании. Сторона AB равна , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ. а) Докажите, что точка P является серединой отрезка BQ. б) Найдите угол между плоскостями SBA и SBC, если ребро SD равно 9.
Объяснение:
а) т. к. S проектируется в центр, то пусть
По теореме косинусов в треугольнике ABS:
откуда следует, что
B прямоугольном Δ ASP:
Аналогично из ΔBCS и прямоугольного ΔCQS находим:
Значит QB=2PB, а так как точка В у отрезков общая и они лежат на одной линии, то т. P - середина BQ.
б) Если ребро SD равно 9, то х=9 и
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях. Такие перпендикуляры у нас уже есть, но для дальнейшего решения, нужно чтобы они сходились к одной точке.
Для этого проведем PC' параллельно QC, C' принадлежит BC, тогда угол APC' — искомый. Поскольку PC' параллелен QC и P — середина QB, то PC' — средняя линия, тогда
В ΔCBQ: ∠Q — прямой,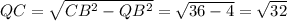 ,
,
тогда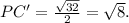
В ΔAPB: ∠P — прямой,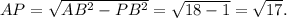
В ΔABC': ∠B — прямой,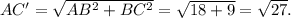
По теореме косинусов в ΔAPC':
Тогда угол между плоскостями SBA и SBC равен
Такой угол больше 90°. А т.к. угол между плоскостями не может превышать 90°, то нам нужен арккосинус смежного угла. Поэтому правильный ответ это: