Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 5 см.
Найди радиус окружности, если известно, что MB равен 25 см и MC равен 5 см.

Показать ответ

Ответ:

ziiaratmagomedova

24.11.2021 03:16

$b(2\sqrt{6}; 2\sqrt{6})$ или $b(-2\sqrt{6}; -2\sqrt{6})$

В пространстве (4; 4; 4) или (-4; -4; -4)

Объяснение:

Пусть вектор b имеет координаты (x; y). Так как координаты по условию равны, то можно записать b(x; x).

Модуль вектора - это его длина, которую находят по формуле: квадратный корень из суммы квадратов координат, что записывается так:

$|b| = \sqrt{x^{2} + x^{2}} = 4\sqrt{3}$

Решаем уравнение относительно x:

$\sqrt{x^{2} + x^{2}} = 4\sqrt{3}\\\\\sqrt{2x^{2}} = 4\sqrt{3}\\\\$

Возводим обе части уравнения в квадрат:

$(\sqrt{2x^{2} })^{2} = (4\sqrt{3} )^{2}\\\\2x^{2} = 16*3\\\\x^{2} = 24\\\\x_{1} = \sqrt{24} = 2\sqrt{6}\\\\ x_{2} = -2\sqrt{6}$

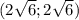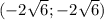
Значит координаты вектора $(2\sqrt{6}; 2\sqrt{6})$ или $(-2\sqrt{6}; -2\sqrt{6})$

P.S. Если вектор в пространстве, то он имеет 3 координаты, тогда уравнение имеет вид:

$\sqrt{x^{2} + x^{2} + x^{2}} = 4\sqrt{3}\\\\\sqrt{3x^{2}} = 4\sqrt{3}\\\\3x^{2} = 16*3\\x^{2} = 16\\x_{1} = 4\\x_{2} = -4$

Значит вектор имеет координаты (4; 4; 4) или (-4; -4; -4)

0,0(0 оценок)

Ответ:

Linarikkomarik

13.04.2023 11:41

Вариант "В"

Объяснение:

Все углы любого треугольника в сумме составляют 180°

Так как заданный треугольник - прямоугольный, то его прямой угол равен 90°, а другие два должны в сумме составлять также 90° (180°-90°=90°), поэтому вариант "А" не подходит (сумма углов 50°+80°=130°)

У нас есть катет a=5см и катет b=8см.

Отношение отношение противолежащего катета к прилежащему - это тангенс угла.

tg(α) = a/b = 5/8 = 0,625 ; atg(0,625) = 32°

tg(β) = b/a = 8/5 = 1,600 ; atg(1,600) = 58°

Из предоставленных вариантов только в варианте "B" есть углы 32° и 58°.

0,0(0 оценок)

Популярные вопросы: Геометрия