Дана окружность радиуса 6 см и точка А на расстоянии равном 7 см от центра окружности. Найдите радиус окружности с центром в точке А и касающейся данной
окружности:
а) касаются внешним образом;
б) касаются внутренним образом?

​

s=235.2 cм2

Объяснение:

обозначив третью сторону с, можно определить что она состоит из двух отрезков разделенных биссектрисой в отношении 14/35, отсюда с=49а.

Рассмотрев два треугольника с одинаковыми углами, определим по теореме косинусов длину этих отрезков составив систему уравнений

(14а)^2=14^2+12^-2*14*12соsα

(35a)^2=35^2+12^-2*35*12соsα

Умножив первое уравнение на 35^2, а второе на 14^2, вычтем одно из другого найдем соsα

α=53,13° Полный угол 106,26°

третья сторона по теореме косинусов

с=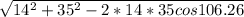=41.2 cм

площадь находим по трем сторонам

p =  ( a + b + c) /2  =   1/ 2  (14 + 35 + 41.2) = 45.1 cм

S = √p(p - a)(p - b)(p - c) =

= √(45.1)(45.1 - 14)(45.1 - 35)(45.1 - 41.2) =

= √(45.1)·(31.1)·(10.1)·(3.9) = √55248.8079 =   √552488079 100  ≈ 235,2 см2

S(трап) = 1/2(осн1 + осн 2) * высота; основания есть, высоту надо найти.
Предлагаю, обозначения
АВСД - данная трапеция, (рисуем картину),
АВ=13 см
СД=15 см
ВС=5 см,
АД=19 см
S(ABCD)-?

Решение
Пусть х см = отрезок АН, ( ВН - высота, опущенная из вершины В трапеции); тогда (19-5-х) = 14-х см = РД ( СР высота, опущенная из вершины С).
Так как треугольник АВН ( уг Н=90*) и тр ДСР (уг Р=90*) прямоугольные и высоты в трапеции равны, то выразим высоту трапеции (ВН =СР) по теореме Пифагора из двух указанных треугольников, получаем уравнение:
169-х^2=225-(14-x)^2
169-x2=225-196+28x-x2
28x = 140
x=5 сторона АН треуг АВН

По т Пифагора к тр АВН найдем ВН, получаем:
ВН=√(169-25) = √144 = 12 см - высота трапеции

S(ABCD)= 1/2 * (BC+AD) * BH
S(ABCD) = 1/2 * 24 * 12 = 12*12 =144