Дана пирамида ABCD такая, что в основании находится правильный треугольник ABC, а ребро AD перпендикулярно основанию. Все вершины пирамиды принадлежат сфере с центром в точке O. а) Докажите, что прямая, проходящая через точку O и центр описанной около треугольника ABC окружности, перпендикулярна плоскости ABC. б) Найдите радиус описанной сферы, если AB = 6, а AD = 4.
KK₁ = 3 ед.
Объяснение:
Дано: прямая АВ;
АК=КВ;
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.
АА₁ = 5; ВВ₁ = 11.
Найти: КК₁
Пусть А₁В₁= 2а.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.
Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
АК = КВ ⇒ А₁К₁ = К₁В₁ = а.
Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.
Вертикальные угла равны.
∠1 = ∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔОВВ₁ (по двум углам)
Составим пропорцию:
Пусть А₁О = 5х, тогда ОВ₁ = 11х
Составим уравнение:
⇒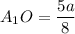
Тогда
Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.
∠1=∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔК₁КО
Составим пропорцию:
234 - 104 = 130 - это сумма двух равных сторон
130 : 2 = 65 - это одна из равных сторон.
Из вершины Δ, противолежащей основанию, опустим высоту на основание
Получим 2 равных прямоугольных треугольника. Рассмотрим один из них.
Высота в равнобедренном Δ является медианой, поэтому высота разделит основание пополам
104 : 2 = 52 - это катет рассматриваемого прямоугольного Δ.
Гипотенуза = боковой стороне = 65
По теореме Пифагора определим другой катет рассматриваемого прямоугольного Δ
Катет = √(65^2 - 52^2) = 39 - это высота равнобедренного Δ
S равнобедренного Δ = 1/2 *39 * 104 = 2028 (кв.ед.)
ответ: 2028 кв.ед - площадь равнобедренного Δ.