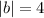Четырёхугольник ABCD - параллелограмм.
∠В - тупой.
∠В = 118°.
Острый угол параллелограмма = ?
Нам дан один тупой угол - это ∠В. А как теперь понять какой ещё тупой угол в этом параллелограмме?
А дело в том, что -
На рисунке ∠В = ∠D = 118°.
Тогда остаётся, что ∠А = ∠С - острые.
То есть -
∠А + ∠В + ∠С + ∠D = 360°
∠А + ∠C = 360° - ∠В - ∠D
∠А + ∠C = 360° - 118° - 118°
∠А + ∠C = 124°
∠A = ∠C = 124° : 2 = 62°.
62°.
Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
, где а - действительная полуось, b - мнимая полуось
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
Также распишем эксцентриситет гиперболы:
Преобразуем. Возведем в квадрат:
Подставим в уравнение с координатами выявленное соотношение:
Все необходимые данные для записи уравнения есть:
Поскольку квадрат мнимой полуоси , то ее длина - соответственно
Четырёхугольник ABCD - параллелограмм.
∠В - тупой.
∠В = 118°.
Найти :Острый угол параллелограмма = ?
Решение :Если в параллелограмме имеется один тупой угол, то в этом параллелограмме есть ещё один тупой угол и два острых угла.Нам дан один тупой угол - это ∠В. А как теперь понять какой ещё тупой угол в этом параллелограмме?
А дело в том, что -
В параллелограмме противоположные углы равны.На рисунке ∠В = ∠D = 118°.
Тогда остаётся, что ∠А = ∠С - острые.
Сумма внутренних углов любого четырёхугольника равна 360°.То есть -
∠А + ∠В + ∠С + ∠D = 360°
∠А + ∠C = 360° - ∠В - ∠D
∠А + ∠C = 360° - 118° - 118°
∠А + ∠C = 124°
∠A = ∠C = 124° : 2 = 62°.
ответ :62°.
Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
Также распишем эксцентриситет гиперболы:
Преобразуем. Возведем в квадрат:
Подставим в уравнение с координатами выявленное соотношение:
Все необходимые данные для записи уравнения есть:
Поскольку квадрат мнимой полуоси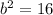 , то ее длина - соответственно
, то ее длина - соответственно