Данные:АС=10 ВD=8 углВОА=60
Найти АВ сторону
найти сторону АВ

Данные:АС=10 ВD=8 углВОА=60Найти АВ сторону найти сторону АВ

Показать ответ

Ответ:

wiryc

08.08.2020 03:11

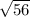AB = AC = $\sqrt{56}$ см

Объяснение:

Дано:

AC = AB, BC = 10 см, BM = 8 см, CM = MA

Знайти: AC,AB - ?

Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =

= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в

точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.

BM = BO + MO;

8 = 2y + y;

8 = 3y;

y =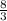 $\frac{8}{3}$ ;

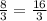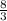BO = 2y = 2 * $\frac{8}{3} = \frac{16}{3}$ ; MO = y = $\frac{8}{3}$ ;

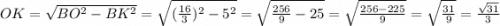За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: $OK = \sqrt{BO^{2} - BK^{2} }=\sqrt{(\frac{16}{3} )^{2} - 5^{2} }=\sqrt{\frac{256}{9} - 25}=\sqrt{\frac{256 - 225}{9} }=\sqrt{\frac{31}{9} }=\frac{\sqrt{31} }{3}$ ;

Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.

AK = OK + AO;

AK = x + 2x = 3x = 3*OK =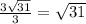 $\frac{3\sqrt{31} }{3} = \sqrt{31}$ ;

За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:

$AB = \sqrt{KA^{2} +KB^{2} }=\sqrt{(\sqrt{31} )^{2} +5^{2} } =\sqrt{31 + 25}=\sqrt{56}$

Так як AB = BC за умовою, то AB = AC =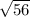 $\sqrt{56}$ см.

за 1 задачу Основа рівнобедреного трикутника дорівнює 10 см, а медіана, проведена до бічної сторони,

0,0(0 оценок)

Ответ:

Karelia1677

29.03.2020 10:25

СДЕЛАЙ ЛУЧШИМ!

В равнобедренном треугольнике боковые стороны равны:

АВ = ВС.

Высота равнобедренного треугольника, выходящая из тупого угла к основанию, делит его пополам:

АД = ДС = АС / 2.

Периметром треугольника является сумма всех его сторон:

Р = АВ + ВС + АС.

Так как длина стороны АС равна сумме отрезков АД и ДС, а сторона АВ у этих треугольников общая, то периметр треугольника АВС будет равен удвоенной сумме сторон АВ и АД:

Р = (АВ + АД) · 2.

Для этого найдем сумму отрезков АВ и АД. Так как периметр треугольника АВД равен 24 см, а сторона ВД равна 8 см, то:

АВ + АД = 24 - 8 = 16 см.

Р = 16 · 2 = 32 см.

ответ: периметр треугольника АВС равен 32 см.

0,0(0 оценок)

Популярные вопросы: Геометрия