Дано ABC=A,B,C BK и B,K соответствующие биссектрисе. Доказать BK= B,K ​

1) BM≈10

2)cosα=0

Объяснение:

1)

Дано трикутник ABC

A(0;-3;-1)

B(-4;0;2)

С(8;3;-7)

BM-медіанна

AC(8-0;3-(-3);-7-(-1)) AC(8;6;-6)

М-середина AC

M(8/2;6/2;-6/2) M(4;3;-3)

BM(4-(-4);3-0;-3-2) BM(8;3;-5)

|BM|=√(8²+3²+(-5)²)=√(64+9+25)≈10

2)

M(0;1;-1) B(1;-1;2) C(3;1;0) D(2;1;1)

MD(2-0;1-1;1-(-1)) MD(2;0;2)

BC(3-1;1-(-1);0-2) BC(2;2;-2)

Знайдемо скалярний добуток векторів:

MD·BC=2·2+02+2·(-2)=4+0-4=0

Знайдемо довжини векторів:

|MD|=√(2²+0²+2²)=√(4+0+4)=√8=2√2

|BC|=√(2²+2²+(-2)²)=√(4+4+4)=√12=2√3

Знайдемо кут між векторами:

cosα=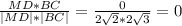

ΔАВС- равнобедренный.Пусть  АВ=ВС =а. ВЕ⊥ АС=10 см, DC⊥АВ=12 см. Найти R окр.,описанной около Δ СDB.
ΔCDB - прямоугольный. R=1/2·BC.(Радиус окружности ,описанной около прямоугольного треугольника = половине гипотенузы)
S(ΔDBC)/S(ΔABC) = DB·BC/AB·BC   ⇒  S(ΔDBC)/S(ΔABC) = DB/BC (1)
S(ΔDBC)=1/2 DB·DC=1/2·DB·12=6·DB                S(ΔDBC) = 6·DB
S(ΔABC)=1/2 AC·BE =1/2AC·10= 5·AC                 S(ΔABC)=5·AC
Получили,что S(ΔDBC)/ S(ΔABC) = 6·DB /5·AC  (2)
Следовательно, DB / BC = 6·DB / 5·AC      ⇒ 5AC=6BC  (3)
Из  Δ ВЕС  найдём  ЕС =х по т. Пифагора : ЕС²=ВС²-ВЕ²
х²=а²-10² ⇒ х=√а²-100     АС=2х=2·√а²-100
Используем (3) равенство :  5 АС=6 ВС и  АС=2х   ⇒
5·2√а²-100 = 6а  ⇒  100·(а²-100)=36 а²  ⇒  64 а²=10000  
а²=10000 / 64   ⇒  а=100 / 8    R = 1/2 a   =  50/8 = 25 / 4