Дано: CDEF ромб, DF диагонали, угол EFD=42градусов. Найти углы треугольника CED

Показать ответ

Ответ:

Анндрейй

10.03.2023 01:51

Объяснение:

Обозначим стороны треугольника

3,5 = а

1,2 = b

3,7 = c

Согласно обратной Т. Пифагора,

если для треугольника со сторонами а, b, c

выполняется равенство:

${a}^{2} + b^{2} = c^{2}$

то этот треугольник - прямоугольный,

с катетами а, b и гипотенузой c

Очевидно, что гипотенуза - длиннее каждого из катетов.

В нашем случае, если треугольник прямоугольный, то его гипотенуза равна 3,7, а катеты 3,5 и 1,2

Проверим выполнение равенства:

$3.5 ^{2} + 1.2 ^{2} = 12.25 + 1.44 = 13.69$

$3.7 ^{2} = 3.7 \times 3.7 = {13.69}$

Следовательно,

$3.5 ^{2} + 1.2 ^{2} = 3.7 ^{2}$

а значит треугольник - прямоугольный

Обозначим искомую высоту, проведённую к большей стороне как h и найдем ее через площадь.

Площадь прямоугольного треугольника равна:

1) половине произведения катетов

$S = \frac{1}{2} \cdot {a}\cdot {b}$

2) Половине произведения гипотенузы на высоту, к ней опущенную:

$S = \frac{1}{2} \cdot {c}\cdot {h}$

Отсюда:

$\tfrac{1}{2} {a}{b} = \tfrac{1}{2} {c}{h} < = ab = ch < = h = \frac{ab}{c} \\$

Вычислим значение h

$h = \frac{3.5 {\cdot} 1.2}{3.7} = \frac{4.2}{3.7} = \frac{42}{37} = 1 \frac{5}{37} \approx1.135 \\$

0,0(0 оценок)

Ответ:

DenisMarvin

02.05.2023 18:46

9.6

Объяснение:

Проведем две высоты в трапеции, как приведено на рисунке. Отрезок, заключенный между высотами, по теореме Фалеса будет одним и тем же, то есть равным 6 см, значит оставшаяся часть - это 20 см. Если за x обозначить одну из частей, тогда 20 - x будет второй фрагмент этих 20 см.

Рассматривая прямоугольные треугольники и взяв на вооружение тот факт, что высота в данной трапеции будет одинаковой, можно решить уравнение:

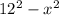12^2 - x^2 = 16^2 - (20 - x)^2