Дано паралельні площини a і b. Точки M i N лежать у площині а, точки K i P — у площині b (рис. 31.9). Побудуйте лінію перетину: 1) площини a і площини МКР; 2) площини b i площини MNK.
Решим данную задачу алгебраическим через уравнение).
Формула периметра тр-ка:
Алгебраический решения задачи:
Пусть x (см) равна боковая сторона, тогда основание будет равно (x-14) (см). Т.к. боковые стороны равнобедренного тр-ка равны, то вторая боковая сторона тоже x (см). Периметр тр-ка равен 76 (см).
I этап. Составление математической модели:
II этап. Работа с математической моделью:
III этап. ответ математической модели:
(см) равна боковая сторона.
IV этап. ответ на вопрос задачи:
Т.к. боковые стороны равны, то их сумма равна 30+30=60 (см).
Тогда основание равно: 76-60=16 (см) или 30-14=16 (см).
Проверка:
По правилу сумма двух сторон тр-ка должна быть больше одной стороны.
Здравствуйте, Jdirjmnab!
Решим данную задачу алгебраическим через уравнение).
Формула периметра тр-ка: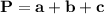
Алгебраический решения задачи:Пусть x (см) равна боковая сторона, тогда основание будет равно (x-14) (см). Т.к. боковые стороны равнобедренного тр-ка равны, то вторая боковая сторона тоже x (см). Периметр тр-ка равен 76 (см).
I этап. Составление математической модели:
II этап. Работа с математической моделью:
III этап. ответ математической модели:
IV этап. ответ на вопрос задачи:
Т.к. боковые стороны равны, то их сумма равна 30+30=60 (см).
Тогда основание равно: 76-60=16 (см) или 30-14=16 (см).
Проверка:По правилу сумма двух сторон тр-ка должна быть больше одной стороны.
30+30>16 - верно; 30+16>30 - верно; 30+16>30 - верно.
Окончательный ответ задачи:В данном тр-ке: "боковые стороны по 30 (см), основание 16 (см).
С Уважением, NeNs07.
Объяснение:
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом.
У прямоугольного параллелепипеда все грани — прямоугольники.
Длина вектора равна длине отрезка ( над векторами нужно ставить стрелки).
|BB₁ |=12 ( противоположные ребра равны) ;
|AD|=11 ;
|CD₁ |=√153 ( из прямоугольного ΔDСD1 пот. Пифагора CD₁²=3²+12²) ;
|BD|=√130 ( из прямоугольного ΔАВD пот. Пифагора CD₁²=3²+11²) ;
| BD₁ |= √146 (Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений: BD₁²=3²+4²+11² , BD₁²=146 )