Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?
Объяснение:
Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).
Меншою діагоналлю паралелепіпеда буде та, яка проектується на меншу діагональ основи, тобто та, що лежить проти кута 45°. Отже менша діагональ основи ВD, а менша діагональ паралелепіпеда В1D = 7 см.
Внутри правильного треугольника со стороной √3 выбрана произвольная точка . Чему равна сумма расстояний от этой точки до сторон треугольника ?
Объяснение:
Пусть точка Р-произвольная. Опустим на стороны правильного ΔАВС перпендикуляры . Обозначим их х,у,z ( кстати, получили педальный треугольник, если соединить основания перпендикуляров).
S(ABC)=S( PAB)+S(PBC)+S(PAC).
S(ABC)=S(равн. тр)=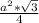 =
=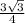 ,
,
S( PAB)=1/2*a*h=1/2*√3*x,
S(PBC)=1/2*a*h=1/2*√3*y,
S(PAC)=1/2*a*h=1/2*√3*z.
x+y+z=1,5
Так як паралелепіпед прямий, то ∆ ВDВ1 прямокутний з гіпотенузою В1D. За теоремою Піфагора знайдемо висоту В1В паралелепіпеда: В1В2 = В1D2 – BD2 = 72 – 13 = 49 – 13 = 36. В1В = 6 см. SABCD = AB ∙ AD ∙ sin ∠BAD = 2√2 ∙ 5 ∙ √2 2 = 10 (см2).
Знаходимо об’єм паралелепіпеда: V = SABCD ∙ BB1 = 10 ∙ 6 = 60 (см3).
Нехай АВ = 2√2 см, АD = 5 см, ∠BAD = 45°.
Меншою діагоналлю паралелепіпеда буде та, яка проектується на меншу діагональ основи, тобто та, що лежить проти кута 45°. Отже менша діагональ основи ВD, а менша діагональ паралелепіпеда В1D = 7 см.
За теоремою косинусів:
ВD. BD2 = AB2 + AD2 – 2 ∙ AB ∙ AD ∙ cos∠BAD = = (2√2)2 + 52 – 2 ∙ 2√2 ∙ 5 ∙ cos45° = = 8 + 25 - 20√2 ∙ √2 2 = 33 – 20 = 13.