Объем - это площадь основания на высоту. Площадь основания есть площадь ромба, а высоту можешь найти исходя из того, что диагональные сечения есть прямоугольники, ширина обеих - высота, а длины равны длинам соответствующих диагоналей. Произведение диагоналей находишь из определения площади ромба. S= произведение диагоналей делённое пополам, то есть ab/2. Отсюда ab=60. Это же произведение можно ещё представить, как (96/h) *(40\h) = 3840/(h^2), где h - высота
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=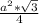
⇒ S(равн.треуг.)= 
= 
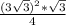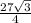(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.
3840/h^2 = 60, откуда h^2 = 64, откуда h=8.
Объем равен 30*8 = 240