Дано треугольник abc равнобедренный ab=10 bc=15 bp=7 ap=5 найти косинус большeго угла треугольника cpb

ответ: 36см

Дано: ABCD- прямоугольник, ∠ВОС=120°, АВ=18см

Найти АС-?

Решение: Свойства диагоналей прямоугольника:

Диагонали прямоугольника  равны  и в точке пересечения делятся пополам.

АО=ВО.

Вариант 1 :

∠ВОС и ∠АОВ- смежные, поэтому  ∠АОВ=180°-∠ВОС=180°-120°=60°

Рассмотрим ΔАОВ, АО=ВО, соответственно ∠ОАВ=∠ОВА, как углы при основании равнобедренного треугольника.

По теореме о сумме трех углов треугольника 2*∠ОАВ+∠АОВ=180°,→

∠ОАВ=(180°-∠АОВ):2=(180°-60°)=60°

следовательно ΔАОВ-равносторонний АО=18см

АС=АО+ОС=2АО=2*18=36(см)

Вариант 2.

Рассмотрим ΔАОВ. ∠ВОС=120°- внешний угол при вершине равнобедренного треугольника( АО=ВО)

∠ОАВ+∠ОВА=∠ВОС;

2*∠ОАВ=120°;

∠ОАВ=60°, следовательно ΔАОВ-равносторонний АО=18см

АС=АО+ОС=2АО=2*18=36(см)

1. Противоположные стороны параллелограмма попарно равны.

2. Противоположные углы параллелограмма попарно равны.

3. Сумма градусных мер двух смежных углов параллелограмма равна 180°.

4. Сумма всех углов параллелограмма равна 360°.

5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

6. Точка пересечения диагоналей является центром симметрии параллелограмма.  

7. Диагонали  d₁ и d₂ и стороны  a и b параллелограмма связаны следующим соотношением: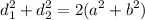    

8. Биссектриса отсекает от параллелограмма равнобедренный треугольник.