103. Поскольку ММ1 = 5 см, КК1 = 11 см, а угол КМ1К1 = 45°, можно сделать вывод, что угол КМ1М = 45°, ведь 90-45=45. Когда стороны ММ1 и КК1 не равны, но являются перпендикулярами одной прямой, можно говорить, что сторона МК не параллельна прямой, а из этого можно сделать вывод по определению прямоугольной трапеции (угол при одной из основ 90°, две стороны параллельны, две нет). ответ на первый вопрос: Прямоугольная трапеция.
Поскольку площадь прямоугольной трапеции определяется по формуле , где а - малое основание, с - большое основание а b - перпендикулярная основам сторона, можно сложить выражение, учитывая то, что сторона КК1 = М1К1 ведь треугольник М1К1К - равнобедренный (90-45=45). Таким образом мы узнаем высоту. И наконец складываем уравнение: , где решением будет 88 см².
104. Для начала стоит визуализировать данную информацию, что вы можете увидеть на прикреплённом файле. МP = 8, PK = 14, MH = 12, KH = 10. В прямоугольной трапеции, (доводим так-же, как в номере 103), есть две основы , которые равняются 7 и 12 см, и высота = 10 см. Складываем формулу (из номера 103) и получаем результат: 95 см².
PS. Скорее всего условие задачи 104 неверное, ведь написано прямоугольник (а у него каждые 2 стороны равны и параллельны), и тут же говорится что PK = 14 а MH = 12, что невозможно. Если взять за вторую основу 14 см, в конечном итоге выходит 105, но увы, уже тебе решать что из этого стоит написать в ответ.
103. Поскольку ММ1 = 5 см, КК1 = 11 см, а угол КМ1К1 = 45°, можно сделать вывод, что угол КМ1М = 45°, ведь 90-45=45. Когда стороны ММ1 и КК1 не равны, но являются перпендикулярами одной прямой, можно говорить, что сторона МК не параллельна прямой, а из этого можно сделать вывод по определению прямоугольной трапеции (угол при одной из основ 90°, две стороны параллельны, две нет). ответ на первый вопрос: Прямоугольная трапеция.
Поскольку площадь прямоугольной трапеции определяется по формуле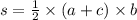
, где а - малое основание, с - большое основание а b - перпендикулярная основам сторона, можно сложить выражение, учитывая то, что сторона КК1 = М1К1 ведь треугольник М1К1К - равнобедренный (90-45=45). Таким образом мы узнаем высоту. И наконец складываем уравнение: 
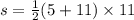, где решением будет 88 см².
104. Для начала стоит визуализировать данную информацию, что вы можете увидеть на прикреплённом файле. МP = 8, PK = 14, MH = 12, KH = 10. В прямоугольной трапеции, (доводим так-же, как в номере 103), есть две основы , которые равняются 7 и 12 см, и высота = 10 см. Складываем формулу (из номера 103) и получаем результат: 95 см².
PS. Скорее всего условие задачи 104 неверное, ведь написано прямоугольник (а у него каждые 2 стороны равны и параллельны), и тут же говорится что PK = 14 а MH = 12, что невозможно. Если взять за вторую основу 14 см, в конечном итоге выходит 105, но увы, уже тебе решать что из этого стоит написать в ответ.
Треугольник АВС
Высота ВН делит его на два прямоугольных треугольника АВН и СВН, где АВ и ВС - гипотенузы.
Примем АН за х.
Тогда СН = АС-х
Составляем два уравнения:
Для треугольника АВН:
ВН^2 = АВ^2 - х^2
Для треугольника СВН:
ВН^2 = ВС^2 - (АС -х)^2
Так как левые части этих уравнений равны, то равны и правые.
АВ^2 - х^2 = ВС^2 - (АС -х)^2
АВ^2 - х^2 - ВС^2 + АС^2 -2АС•х + х^2 = 0
2х•АС = АВ^2 - ВС^2 + АС^2
х = (АВ^2 - ВС^2 + АС^2) / 2АС
Тогда значение х можно вставить в уравнение:
ВН^2 = АВ^2 - х^2
ВЕ^2 = АВ^2 - ((АВ^2 - ВС^2 + АС^2) / 2АС)^2
Объяснение: