Из комментария к вопросу - исправленное условие. Две плоскости параллельны между собой. С точки К, которая не лежит в этих плоскостях или между ними, проведены две прямые, которые пересекают эти плоскости соответственно в точках А1 и А2 и В1 и В2. КА1=3 см, В1В2=12 см, А1А2=КВ1. Найти КА2.
Через три точки можно провести плоскость.⇒
Все точки прямых КА2 и КВ2 лежат в одной плоскости. Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. ⇒А1В1|║А2В2.
Треугольники КА2В2 и КА1В1 подобны по равным углам.
MP - средняя линия трапеции ABCD ( по определению средней линии: отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции )
Длинна средней линии находится по формуле ⇒
ответ: AD = 1
P.s - мне кажется, правильнее было бы верхнее основанее назвать AD, а нижнее BC ( так как верхнее основанее не может быть больше средней линии, а нижнее не может быть меньше)
Через три точки можно провести плоскость.⇒
Все точки прямых КА2 и КВ2 лежат в одной плоскости. Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. ⇒А1В1|║А2В2.
Треугольники КА2В2 и КА1В1 подобны по равным углам.
Из подобия следует
КА2:КА1=КВ2:КВ1
Обозначим А1А2=КВ1=а
Тогда (а+3):а=(а+12):а ⇒
а²=36, а=√36=6 см
КА2=КА1+А1А2=9 см
Дано: ABCD - трапеция
AM = MB
CP = PD
BC // MP // AD
MP = 3
BC = 5
Найти: AD
MP - средняя линия трапеции ABCD ( по определению средней линии: отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции )
Длинна средней линии находится по формуле ⇒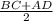
ответ: AD = 1
P.s - мне кажется, правильнее было бы верхнее основанее назвать AD, а нижнее BC ( так как верхнее основанее не может быть больше средней линии, а нижнее не может быть меньше)
⇒ фото чтобы вы поняли, что я имею ввиду