Рассмотрим треугольник АВС, у которого АВ≠ВС, ВС≠АС, АВ ≠ АС, пусть ВН - высота ∆ АВС, ВD - биссектриса ∆ АВС, ВМ -медиана ∆ АВС.
НЕ ограничивая общности будем считать, что ВС<АВ, тогда, по доказанному в задаче №346, получим, что точка Н принадлежит лучу
По доказанному в задаче №341, получим, что АD>DС, но
АD+DС=АС, следовательно,
ВМ - медиана, следователь
Получем, что АD>АМ, т.е. точка М при
надлежит отрезку АD, следовательно, точка М принадлежит отрезку АD, следовательно, точка М принадлежит лучу DА, а точка О лежит между точками Ни М, что и требовалось доказать.
45°
Объяснение:
АВСД-ромб. АС⊥ВД. АС=40см. ВД=30см.
Из вершины В ромба АВСД проведём высоту ВК⊥ДС.
МК - наклонная, ВК - её проекция на плоскость АВСД.
По теореме о трёх перпендикулярах: МК⊥ДС.
∠МКБ - угол между плоскостью ромба и плоскостью CMD - искомый угол.
(Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.)
1) ΔОВС (∠О=90° - как угол между диагоналями ромба).
По т.Пифагора найдём сторону ромба:
ВС² = ВО²+ОС² = 15²+20²=625, ВС= 25 см
Т.е. АВ=ВС=СД=АД=25 см - как диагонали ромба
2) ΔВСД .
СО⊥ВД т.к. диагонали ромба пересекаются под прямым углом.
ВК⊥ДС по построению.
Площадь ΔВСД:
S =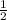
*ВД*ОС
S =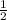
*ДС*ВК
⇒ВД*ОС=ДС*ВК; 30*20=25*ВК; ВК=30*20/25=24 см
3) Рассмотрим ΔМВК. МВ⊥ВК, МВ=ВК=24 см.
⇒ΔМВК - равносторонний прямоугольный треугольник.
∠КМВ =∠МКВ = 90°/2 = 45°
Объяснение:
Привет. Вот там какое решение
Рассмотрим треугольник АВС, у которого АВ≠ВС, ВС≠АС, АВ ≠ АС, пусть ВН - высота ∆ АВС, ВD - биссектриса ∆ АВС, ВМ -медиана ∆ АВС.
НЕ ограничивая общности будем считать, что ВС<АВ, тогда, по доказанному в задаче №346, получим, что точка Н принадлежит лучу
По доказанному в задаче №341, получим, что АD>DС, но
АD+DС=АС, следовательно,
ВМ - медиана, следователь
Получем, что АD>АМ, т.е. точка М при
надлежит отрезку АD, следовательно, точка М принадлежит отрезку АD, следовательно, точка М принадлежит лучу DА, а точка О лежит между точками Ни М, что и требовалось доказать.