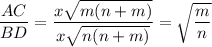Дано зображення трикутної піраміди SABC, де точки D, HiM на- лежать ребрам АС, SB i SA відповідно. Скільки можна провести пло- щин через точки Вопрос: S, Mi B?
1) В прямоугольном треугольнике АВС из вершины прямого угла С проведем к гипотенузе AB отрезок CO так, чтобы CO=OA.
2) ∆ AOC — равнобедренный с основанием AC (по определению равнобедренного треугольника).
Значит, у него углы при основании равны:∠OAC=∠OCA=α.
3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в треугольнике ABC ∠B=90º- α.
4) Так как ∠BCA=90º (по условию), то ∠BCO=90º- ∠OCA=90º-α.
5) Рассмотрим треугольник BOC.
∠BCO=90º-α, ∠B=90º- α, следовательно, ∠BCO=∠B.
Значит, треугольник BOC — равнобедренный с основанием BC (по признаку равнобедренного треугольника).
Отсюда BO=CO.
6) Так как CO=OA (по построению) и BO=CO (по доказанному), то CO=OA=BO, AB=OA+BO=2∙OA=2∙CO.
Таким образом, точка O — середина гипотенузы AB, отрезок CO соединяет вершину треугольника с серединой противолежащей стороны, значит, CO — медиана, проведенная к гипотенузе, и она равна половине гипотенузы
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
1) В прямоугольном треугольнике АВС из вершины прямого угла С проведем к гипотенузе AB отрезок CO так, чтобы CO=OA.
2) ∆ AOC — равнобедренный с основанием AC (по определению равнобедренного треугольника).
Значит, у него углы при основании равны:∠OAC=∠OCA=α.
3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в треугольнике ABC ∠B=90º- α.
4) Так как ∠BCA=90º (по условию), то ∠BCO=90º- ∠OCA=90º-α.
5) Рассмотрим треугольник BOC.
∠BCO=90º-α, ∠B=90º- α, следовательно, ∠BCO=∠B.
Значит, треугольник BOC — равнобедренный с основанием BC (по признаку равнобедренного треугольника).
Отсюда BO=CO.
6) Так как CO=OA (по построению) и BO=CO (по доказанному), то CO=OA=BO, AB=OA+BO=2∙OA=2∙CO.
Таким образом, точка O — середина гипотенузы AB, отрезок CO соединяет вершину треугольника с серединой противолежащей стороны, значит, CO — медиана, проведенная к гипотенузе, и она равна половине гипотенузы
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.
Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
Следовательно,