Даны 3 последовательные вершины параллелограмма а(3; -2), b(-4,3),c(-1; 6).не находя координаты вершины d, найти:
1) уравнение стороны ad
2)уравнение высоты bk, опущенной из вершины b на сторону ad
3)длину высоты bk
4)уравнение диагонали bd
5)тангенс угла между диагоналями параллелограмма
записать общие уравнения найденных прямых. построить чертеж
1. Радиус сферы равен половине диаметра, R = 25 см.
Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен сечению. это и есть расстояние от центра сферы до сечения.
Итак, ОА = 25 см, ОС = 15 см. Из прямоугольного треугольника АОС по теореме Пифагора находим радиус сечения:
АС = √(ОА² - ОС²) = √(25² - 15²) = √(625 - 225) = √400 = 20 cм
Линия пересечения сферы плоскостью - окружность. Ее длина:
C = 2π·AC = 2π · 20 = 40π см
2. Сечение шара - круг. Его площадь равна 36π см²:
Sсеч = π · r² = 36π
r² = 36
r = 6 см
Из прямоугольного треугольника АОС по теореме Пифагора:
ОС = √(ОА² - r²) = √(100 - 36) = √64 = 8 см - искомое расстояние.
3. Радиус большого круга равен радиусу шара.
Площадь сечения:
Sсеч = πr²
Площадь большого круга:
S = πR², R = √(S/π)
Sсеч / S = πr² / (πR²) = r²/ R²
По условию Sсеч / S = 3 / 4, ⇒
r²/ R² = 3 / 4, тогда r/R = √3/2
В прямоугольном треугольнике АОС r/R - это косинус угла А.
Тогда ∠А = 30°.
Расстояние от центра шара до сечения - отрезок ОС. Это катет, лежащий напротив угла в 30°, значит он равен
OC = R/2 = √(S/π) / 2 = √S/(2√π)
4. Радиус шара равен половине диаметра:
R = 2√3 см
Прямоугольный треугольник ОВС равнобедренный, так как в нем острый угол равен 45°, поэтому
ОС = r = R/√2 = 2√3 / √2 = √6 см
Sсеч = πr² = π · (√6)² = 6π см²
1. Могут.
2. б) 6 см
3. б) 45°
Объяснение:
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б)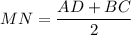
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
а) ВС лежит в плоскости (АВС),
МА пересекает (АВС) в точке А,
А не лежит на прямой ВС, значит
МА и ВС скрещивающиеся.
б) ∠(МА, AD) = 45° по условию,
BC║AD, значит
∠(МА, ВС) = 45°