1. Одна сторона = х см, другая сторона = 2х см х+х+2х+2х=48 6х=48 х=8 8 см одна сторона 8*2=16 см другая сторона
2. Параллелограмм АBCD, биссектриса АК Угол ВАК = углу КАD, т.к. биссектриса АК делит угол ВАD пополам. Угол КAD = углу BKA, т.к. они накрест лежащие при AD параллельном ВС и секущей АК. Значит, угол ВАК = углу ВКА, т.к. все эти три угла равны между собой. Значит, треугольник АВК равнобедренный, т.к. углы при основании равны. Значит, АВ=ВК=7 см
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC , ,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
х+х+2х+2х=48
6х=48
х=8
8 см одна сторона
8*2=16 см другая сторона
2. Параллелограмм АBCD, биссектриса АК
Угол ВАК = углу КАD, т.к. биссектриса АК делит угол ВАD пополам.
Угол КAD = углу BKA, т.к. они накрест лежащие при AD параллельном ВС и секущей АК.
Значит, угол ВАК = углу ВКА, т.к. все эти три угла равны между собой.
Значит, треугольник АВК равнобедренный, т.к. углы при основании равны.
Значит, АВ=ВК=7 см
7+14=21 см другая сторона параллелограмма
7+7+21+21=56 см периметр параллелограмма.
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC ,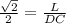
,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
И ΔВCD-равнобедренный ⇒ВD=DС=L√2.
Значит АВ=2L√2.
S=1/2*a*h , S(АВС)=1/2*2L√2*L√2=2L² .