Даны шесть отрезков длиной 3см; шесть отрезков длиной 7см; шесть отрезков длиной 8см. с использованием части из этих отрезков сконструирована треугольная прямая призма. вычисли максимальный возможный объём этой призмы.
запиши, чему равны cтороны основания призмы (в возрастающем/неубывающем порядке):
высота призмы равна
mаксимальный возможный объём этой призмы равен
v=
Шар вписан в конус. найти наименьший объём конуса, если радиус шара равен 1.
Решение.
1) Рассмотрим осевое сечение данной комбинации тел : равнобедренный ΔАВС , высота ВН , точка О-центр вписанной окружности. К-точка касания окружности со стороной АВ. По условию ОН=ОК=1 ед.
Пусть ВН=h , AH=R. Vкон=1/3*Sосн*h , Sосн=π*R²
Выразим объём через высоту конуса.
Отрезок ВО=ВН-ОН=h-1
По т. Пифагора , ΔABH , АВ²=АН²+ВН²=R²+h² .
2) ΔКВО~ ΔHBA по двум углам(∠В-общий,∠ВКО=АНВ=90° тк радиус перпендикулярен касательной , проведенной в точку касания).
Значит КО:АН=ВО:АВ или 1:R=(h-1): √(R²+h²) ⇒ R²=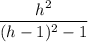
.
3) V(h)=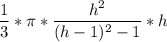
= 
= 
.
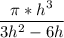V' =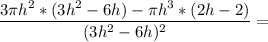
=
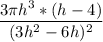, V'=0, при h=4 .
V' _ _ _ _(4) + + + +
V ↓ ↑ , значит h=4 точка минимума. Наименьший объём достигается в точке минимума .
V =
⇒ V=
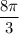ед³ .
Відповідь:
51 прямоугольник.
Пояснення:
Пояснение: Например прямоугольник 1.2 - прямоугольник включающий в себя два прямоугольника 1 и 2.
1) 1
2) 2
3) 3
4) 4
5) 1.2
6) 2.3
7) 3.4
8) 1.2.3
9) 2.3.4
10) 1.2.3.4
11) 5
12) 6
13) 7
14) 8
15) 5.6
16) 6.7
17) 7.8
18) 5.6.7
19) 6.7.8
20) 5.6.7.8
21) 1.5
22) 2.6
23) 3.7
24) 4.8
25) 1.2.5.6
26) 2.3.6.7
27) 3.4.7.8
28) 1.2.3.5.6.7
29) 2.3.4.6.7.8
30) 1.2.3.4.5.6.7.8
31) 9
32) 10
33) 9.2
34) 6.10
35) 9.2.6
36) 2.6.10
37) 9.2.6.10
38) 11
39) 12
40) 11.3
41) 7.12
42) 11.3.7
43) 3.7.12
44) 11.3.7.12
45) 9.11
46) 10.12
47) 9.11.2.3
48) 6.7.10.12
49) 9.11.2.3.6.7
50) 2.3.6.7.10.12
51) 9.11.2.3.6.7.10.12