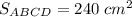Даны точка C, лежащая на прямой AB, и точка E, не лежащая на прямой. Какая связь между линиями ЕС и АВ? Рассмотрим две ситуации.

Показать ответ

Ответ:

Sofia621

05.11.2020 20:29

1) а) Найдем углы в треугольнике АСО. Угол АОС равен (180-128)/2.

Т.к. односторонние сумма углов равна 180 градусам. А биссектриса делит угол пополам.

Угол САО равен 128. Т.к. его вертикальный угол равен 128, а вертикальные углы равны. А сумма односторонних углов равна 180. Следовательно угол А=128.

Посчитаем угол АСО. Сумма углов треугольника равна 180 градусом. 180-128-26=26.

Углы при основании равны. Значит треугольник АСО равнобедренные, а его боковые стороны АС и АО равны. Чтд.

б) 26

Объяснение:

0,0(0 оценок)

Ответ:

Ясминка2006

07.11.2021 13:12

В ромбе диагонали точкой пересечения делятся пополам (АО=ОС и ВО=OD).

Пусть ВО=х, тогда:

AC-BD=14

AC-2x=14

AC=14+2x

2·OC=2(x+7)

OC=x+7

Из ΔBCO по т. Пифагора:

$\displaystyle BC^2=BO^2+OC^2\\17^2=x^2+(x+7)^2\\x^2+x^2+14x+49=289\\2x^2+14x-240=0\\x^2+7x-120=0\\D=b^2-4ac=7^2-4\cdot 1 \cdot (-120)=49+480=529\\x_1=\frac{-b+\sqrt{D} }{2a} =\frac{-7+23}{2} =8\\x_2=\frac{-b-\sqrt{D} }{2a} =\frac{-7-23}{2}=-15$

x=-15 не подходит по смыслу задачи, поэтому один корень х=8.

ВО=х=8 см

ОС=х+7=8+7=15 см

АС=АО+ОС=15+15=30 см

BD=BO+OD=8+8=16 см

$\displaystyle S_{ABCD}=\frac{AC\cdot BD}{2} =\frac{30\cdot 16}{2} =240\; cm^2$

Вспомним такую формулу: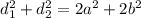 d_1^2+d_2^2=2a^2+2b^2 , где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).

Найдем диагонали, составив систему:

Пусть АС=х, BD=y.

$\displaystyle \left \{ {{AC-BD=14} \atop {AC^2+BD^2=2AB^2+2BC^2}} \right. \\\left \{ {{x-y=14} \atop {x^2+y^2=2\cdot 17^2+2\cdot 17^2}} \right. \\\left \{ {{x-y=14} \atop {x^2+y^2=1156}} \right. \\\left \{ {{x=14+y} \atop {(14+y)^2+y^2=1156}} \right. \\\left \{ {{x=14+y} \atop {196+28y+y^2+y^2=1156}} \right. \\\left \{ {{x=14+y} \atop {y^2+14y-480=0}} \right. \\{\left [ \left \{ {{y=16} \atop {x=30}} \right. \atop\left \{ {{y=-30} \atop {x=-16}} \right. \right.$