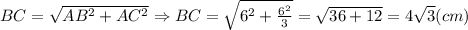Даны точки А (2; 1; 3), В (7; 2; — 3) и С (— 2; 3; 1). Вычислите угол между векторами СА и СВ.

Я опробовала много решения задачи — зная радиус, но в конце концов сделала вывод, что он нам совсем не нужен.

Нам достаточно знать всего лишь отрезки, полученные делением точки касания на гипотенузе.

Теорема о касательных такова: 2 касательные, проведённые с одной точки, в точках касания — равны друг другу.

То есть: BE == BD = 12 (так как оба отрезка проведены с общей точки B).

И ещё: FC == DC = 18 (то же определение).

И также: KE == KF (оба проведены с одной точки (K)).

По теореме Пифагора, гипотенуза равна:

Найдём Дискриминант:

Следовательно:

Следовательно:

Вывод: KC = 24см; BK = 18см; P = 72см.

см

Объяснение:

Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.

І варіант рішення:

1) Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)

2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому

ІІ варіант рішення:

1)  Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

2)  Розглянемо прямокутний ΔКАС.

В ньому ∠С=180°-90°-∠В=60°.

Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)

3)  Розглянемо ΔАВС.

Гіпотенуза