Пусть один из катетов прямоугольного треугольника равен тогда второй —
По теореме Пифагора гипотенуза такого треугольника равна
В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине, т. е.
а высота, проведенная к гипотенузе, вычисляется через формулу т. е.
По условию
Заметим, что дискриминант квадратного трехчлена отрицательный, значит выражение под корнем никогда не превращается в ноль. Умножим обе части уравнения на :
Периметр треугольника равен 120 см.
Объяснение:
Сумма катетов прямоугольного треугольника равна 70 см, а сумма медианы и высоты , проведенных к гипотенузе, равна 49 см . Найти периметр треугольника.
Пусть дан Δ АВС , в котором a и b - катеты , с - гипотенуза .
Тогда а+ b =70 см
Медиану, проведенную к гипотенузе, назовем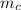 , а высоту, проведенную к гипотенузе назовем
, а высоту, проведенную к гипотенузе назовем 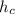
Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то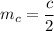
Высота прямоугольного треугольника, проведенная к гипотенузе, определяется по формуле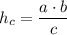
где a,b-катеты , c - гипотенуза.
По условию
Тогда
Теорема Пифагора : в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Подставим в равенство (1) вместо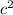 выражение
выражение 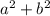
Применим формулу сокращенного умножения
По условию а+ b =70.
Значит, гипотенуза с= 50 см.
Периметр треугольника - это сумма длин всех сторон .
Тогда P=a+b+c
P= 70 + 50 =120 cм
Периметр треугольника равен 120 см
Объяснение:
Пусть один из катетов прямоугольного треугольника равен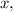 тогда второй —
тогда второй — 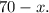
По теореме Пифагора гипотенуза такого треугольника равна
В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине, т. е.
а высота, проведенная к гипотенузе, вычисляется через формулу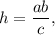 т. е.
т. е.
По условию
Заметим, что дискриминант квадратного трехчлена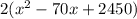 отрицательный, значит выражение под корнем никогда не превращается в ноль. Умножим обе части уравнения на
отрицательный, значит выражение под корнем никогда не превращается в ноль. Умножим обе части уравнения на 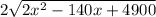 :
:
Значит катеты треугольника 30 и 40, а гипотенуза
Таким образом, периметр треугольника равен