Площадь этой фигуры равна площади равностороннего треугольника (в центре) со сторонами, равными диаметрам окружностей, МИНУС утроенная площадь сектора, образованного радиусами, образующими центральный угол 60° (или МИНУС половина площади одной окружности). Площадь равностороннего треугольника Sтр = (√3/4)*а², (где а - сторона треугольника = 8), Sтр = (√3/4)*8*8 = 16√3. Sсек = (πR²*α)/360,где α = 60°. Тогда (π*16*60)/360 = π*8/3. А три сектора = π*8 ≈ 25,12. Или так: три наших сектора равны половине площади круга, то есть πR²/2=8*π≈ 25,12.
Значит искомая площадь равна 16√3-25,12 ≈ 27,71-25,12 = 2,59.
))) Интересное задание, сначала не хотел браться, потом "зацепило"...
Смотрим рисунок и вспоминаем свойство касательных:
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности (вот почему, собственно, центр вписанной в треугольник окружности лежит в точке пересечения биссектрис...).
Пусть точки М, К и О - точки касания окружности со сторонами АВ, ВС и АС, соответственно.
Из свойства касательных следует, что:
Периметр (пока в рассчётах берём именно периметр Р (большая), а не полупериметр р (малая)):
, значит
Так как , то:
Исходя из вышеприведённых равенств:
Имеем право записать как:
В нижней записи у нас уже фигурирует полупериметр р (малая). ЧТД
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))
Площадь равностороннего треугольника Sтр = (√3/4)*а²,
(где а - сторона треугольника = 8),
Sтр = (√3/4)*8*8 = 16√3.
Sсек = (πR²*α)/360,где α = 60°. Тогда (π*16*60)/360 = π*8/3.
А три сектора = π*8 ≈ 25,12.
Или так: три наших сектора равны половине площади круга, то есть πR²/2=8*π≈ 25,12.
Значит искомая площадь равна 16√3-25,12 ≈ 27,71-25,12 = 2,59.
))) Интересное задание, сначала не хотел браться, потом "зацепило"...
Смотрим рисунок и вспоминаем свойство касательных:
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности (вот почему, собственно, центр вписанной в треугольник окружности лежит в точке пересечения биссектрис...).
Пусть точки М, К и О - точки касания окружности со сторонами АВ, ВС и АС, соответственно.
Из свойства касательных следует, что:
Периметр (пока в рассчётах берём именно периметр Р (большая), а не полупериметр р (малая)):
Так как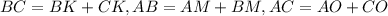 , то:
, то:
Исходя из вышеприведённых равенств:
Имеем право записать как:
В нижней записи у нас уже фигурирует полупериметр р (малая). ЧТД
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))