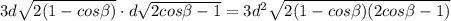Объяснение:
S = Sполн = Sбок + 2Sabc
Из ΔА₁СВ₁ по теореме косинусов найдем сторону основания:
A₁B₁² = d² + d² - 2 · d · d · cosβ = 2d² - 2d²cosβ=2d²(1 - cosβ)
Из ΔАА₁С по теореме Пифагора найдем высоту:
Sбок = Pосн · h
Sбок =
Объяснение:
S = Sполн = Sбок + 2Sabc
Из ΔА₁СВ₁ по теореме косинусов найдем сторону основания:
A₁B₁² = d² + d² - 2 · d · d · cosβ = 2d² - 2d²cosβ=2d²(1 - cosβ)
Из ΔАА₁С по теореме Пифагора найдем высоту:
Sбок = Pосн · h
Sбок =